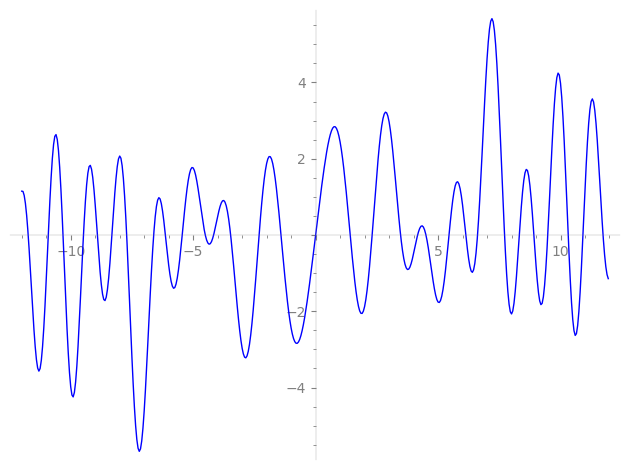
| L(s) = 1 | + 2-s − 4-s + 2·7-s − 3·8-s + 4·11-s + 2·14-s − 16-s + 2·17-s − 8·19-s + 4·22-s − 8·23-s − 2·28-s + 31-s + 5·32-s + 2·34-s − 8·37-s − 8·38-s + 6·41-s − 4·44-s − 8·46-s + 4·47-s − 3·49-s + 6·53-s − 6·56-s − 10·59-s − 14·61-s + 62-s + ⋯ |
| L(s) = 1 | + 0.707·2-s − 1/2·4-s + 0.755·7-s − 1.06·8-s + 1.20·11-s + 0.534·14-s − 1/4·16-s + 0.485·17-s − 1.83·19-s + 0.852·22-s − 1.66·23-s − 0.377·28-s + 0.179·31-s + 0.883·32-s + 0.342·34-s − 1.31·37-s − 1.29·38-s + 0.937·41-s − 0.603·44-s − 1.17·46-s + 0.583·47-s − 3/7·49-s + 0.824·53-s − 0.801·56-s − 1.30·59-s − 1.79·61-s + 0.127·62-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 6975 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 6975 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 3 | \( 1 \) | |
| 5 | \( 1 \) | |
| 31 | \( 1 - T \) | |
| good | 2 | \( 1 - T + p T^{2} \) | 1.2.ab |
| 7 | \( 1 - 2 T + p T^{2} \) | 1.7.ac |
| 11 | \( 1 - 4 T + p T^{2} \) | 1.11.ae |
| 13 | \( 1 + p T^{2} \) | 1.13.a |
| 17 | \( 1 - 2 T + p T^{2} \) | 1.17.ac |
| 19 | \( 1 + 8 T + p T^{2} \) | 1.19.i |
| 23 | \( 1 + 8 T + p T^{2} \) | 1.23.i |
| 29 | \( 1 + p T^{2} \) | 1.29.a |
| 37 | \( 1 + 8 T + p T^{2} \) | 1.37.i |
| 41 | \( 1 - 6 T + p T^{2} \) | 1.41.ag |
| 43 | \( 1 + p T^{2} \) | 1.43.a |
| 47 | \( 1 - 4 T + p T^{2} \) | 1.47.ae |
| 53 | \( 1 - 6 T + p T^{2} \) | 1.53.ag |
| 59 | \( 1 + 10 T + p T^{2} \) | 1.59.k |
| 61 | \( 1 + 14 T + p T^{2} \) | 1.61.o |
| 67 | \( 1 + 2 T + p T^{2} \) | 1.67.c |
| 71 | \( 1 + 6 T + p T^{2} \) | 1.71.g |
| 73 | \( 1 - 16 T + p T^{2} \) | 1.73.aq |
| 79 | \( 1 + p T^{2} \) | 1.79.a |
| 83 | \( 1 - 4 T + p T^{2} \) | 1.83.ae |
| 89 | \( 1 + 4 T + p T^{2} \) | 1.89.e |
| 97 | \( 1 + 6 T + p T^{2} \) | 1.97.g |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−7.71528964305202664128578913928, −6.61182537228330675463218110057, −6.13435314788126744493252717468, −5.44702227752771890436261303291, −4.50499697920881557630168978181, −4.16535865218501984349592475156, −3.47002863835938159210203980612, −2.30822361958007473419290328689, −1.41300095124550131832504594810, 0,
1.41300095124550131832504594810, 2.30822361958007473419290328689, 3.47002863835938159210203980612, 4.16535865218501984349592475156, 4.50499697920881557630168978181, 5.44702227752771890436261303291, 6.13435314788126744493252717468, 6.61182537228330675463218110057, 7.71528964305202664128578913928