↑

Properties

Label 4-61952-1.1-c1e2-0-7
Degree $4$
Conductor $61952$
Sign $-1$
Analytic cond. $3.95011$
Root an. cond. $1.40978$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $1$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

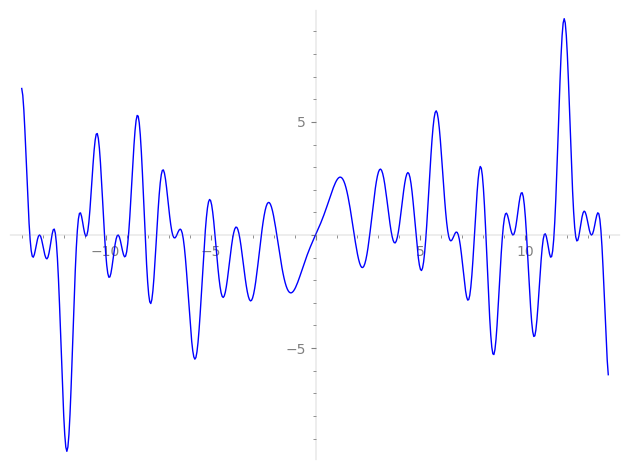
L(s)  = 1  − 4·7-s + 3·9-s − 12·17-s + 2·23-s − 25-s − 14·31-s + 8·41-s − 16·47-s − 2·49-s − 12·63-s + 6·71-s + 32·73-s + 4·79-s + 30·89-s − 14·97-s − 32·103-s − 14·113-s + 48·119-s + 121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s − 36·153-s + 157-s + ⋯
L(s)  = 1  − 1.51·7-s + 9-s − 2.91·17-s + 0.417·23-s − 1/5·25-s − 2.51·31-s + 1.24·41-s − 2.33·47-s − 2/7·49-s − 1.51·63-s + 0.712·71-s + 3.74·73-s + 0.450·79-s + 3.17·89-s − 1.42·97-s − 3.15·103-s − 1.31·113-s + 4.40·119-s + 1/11·121-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s − 2.91·153-s + 0.0798·157-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 61952 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 61952 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(61952\)    =    \(2^{9} \cdot 11^{2}\)
Sign: $-1$
Analytic conductor: \(3.95011\)
Root analytic conductor: \(1.40978\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 61952,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
11$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
good3$C_2$ \( ( 1 - p T + p T^{2} )( 1 + p T + p T^{2} ) \) 2.3.a_ad
5$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.5.a_b
7$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.7.e_s
13$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.13.a_ba
17$C_2$ \( ( 1 + 6 T + p T^{2} )^{2} \) 2.17.m_cs
19$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.19.a_w
23$C_2$ \( ( 1 - T + p T^{2} )^{2} \) 2.23.ac_bv
29$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.29.a_ag
31$C_2$ \( ( 1 + 7 T + p T^{2} )^{2} \) 2.31.o_eh
37$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.37.a_cv
41$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.41.ai_du
43$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.43.a_by
47$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.47.q_gc
53$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.53.a_dy
59$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.59.a_en
61$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.61.a_ec
67$C_2$ \( ( 1 - 5 T + p T^{2} )( 1 + 5 T + p T^{2} ) \) 2.67.a_ef
71$C_2$ \( ( 1 - 3 T + p T^{2} )^{2} \) 2.71.ag_fv
73$C_2$ \( ( 1 - 16 T + p T^{2} )^{2} \) 2.73.abg_pm
79$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.79.ae_gg
83$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.83.a_gg
89$C_2$ \( ( 1 - 15 T + p T^{2} )^{2} \) 2.89.abe_pn
97$C_2$ \( ( 1 + 7 T + p T^{2} )^{2} \) 2.97.o_jj
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−9.424260651660627252011971923444, −9.401670233685537405973889044671, −8.911534990908679817989792101965, −8.118360153173760371978857071616, −7.57356519540538183281509096087, −6.80526418655862410599202441776, −6.61017530637467554226176574176, −6.33216658844039512399715167893, −5.26718062023912132586056594917, −4.78987665155787865457700111621, −3.92131200412791242288608029354, −3.63547474808138538276796488470, −2.58128943528283843865888199294, −1.84559544742735453993387759114, 0, 1.84559544742735453993387759114, 2.58128943528283843865888199294, 3.63547474808138538276796488470, 3.92131200412791242288608029354, 4.78987665155787865457700111621, 5.26718062023912132586056594917, 6.33216658844039512399715167893, 6.61017530637467554226176574176, 6.80526418655862410599202441776, 7.57356519540538183281509096087, 8.118360153173760371978857071616, 8.911534990908679817989792101965, 9.401670233685537405973889044671, 9.424260651660627252011971923444

Graph of the $Z$-function along the critical line