↑

Properties

Label 4-1812608-1.1-c1e2-0-13
Degree $4$
Conductor $1812608$
Sign $-1$
Analytic cond. $115.573$
Root an. cond. $3.27879$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $1$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

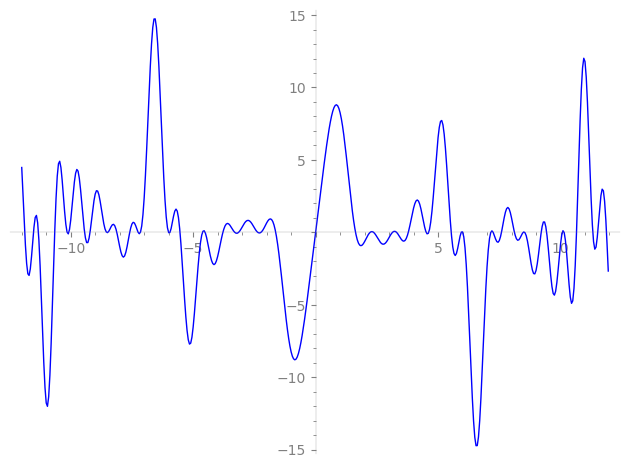
L(s)  = 1  + 2-s + 4·3-s + 4-s + 4·6-s + 8-s + 6·9-s − 4·11-s + 4·12-s + 16-s − 2·17-s + 6·18-s − 4·22-s + 4·24-s − 10·25-s − 4·27-s + 32-s − 16·33-s − 2·34-s + 6·36-s − 4·41-s − 4·44-s + 4·48-s + 49-s − 10·50-s − 8·51-s − 4·54-s + 8·59-s + ⋯
L(s)  = 1  + 0.707·2-s + 2.30·3-s + 1/2·4-s + 1.63·6-s + 0.353·8-s + 2·9-s − 1.20·11-s + 1.15·12-s + 1/4·16-s − 0.485·17-s + 1.41·18-s − 0.852·22-s + 0.816·24-s − 2·25-s − 0.769·27-s + 0.176·32-s − 2.78·33-s − 0.342·34-s + 36-s − 0.624·41-s − 0.603·44-s + 0.577·48-s + 1/7·49-s − 1.41·50-s − 1.12·51-s − 0.544·54-s + 1.04·59-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1812608 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1812608 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(1812608\)    =    \(2^{7} \cdot 7^{2} \cdot 17^{2}\)
Sign: $-1$
Analytic conductor: \(115.573\)
Root analytic conductor: \(3.27879\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 1812608,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_1$ \( 1 - T \)
7$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
17$C_1$ \( ( 1 + T )^{2} \)
good3$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.3.ae_k
5$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.5.a_k
11$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.11.e_ba
13$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.13.a_w
19$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.19.a_bm
23$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.23.a_be
29$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.29.a_bq
31$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.31.a_ck
37$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.37.a_k
41$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.41.e_di
43$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.43.a_di
47$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.47.a_dq
53$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.53.a_dy
59$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.59.ai_fe
61$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.61.a_aw
67$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.67.q_hq
71$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.71.a_ac
73$C_2$ \( ( 1 + 14 T + p T^{2} )^{2} \) 2.73.bc_ne
79$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.79.a_o
83$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.83.ai_ha
89$C_2$ \( ( 1 + 6 T + p T^{2} )^{2} \) 2.89.m_ig
97$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.97.am_iw
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−7.58921476107187061140994872605, −7.24873510617453755225057715176, −7.15338235857431075096387108974, −6.00726227594673864385067167688, −5.94586048673065741845555135065, −5.53703516941704424444929900143, −4.61890591955424914588423851483, −4.51282315413453787474232180705, −3.78506683414990843986999213899, −3.30389600119444587052090687147, −3.14154639715473478514566829712, −2.36560540929594190713679838208, −2.22835033919080433376049523841, −1.63013473710215361786239756870, 0, 1.63013473710215361786239756870, 2.22835033919080433376049523841, 2.36560540929594190713679838208, 3.14154639715473478514566829712, 3.30389600119444587052090687147, 3.78506683414990843986999213899, 4.51282315413453787474232180705, 4.61890591955424914588423851483, 5.53703516941704424444929900143, 5.94586048673065741845555135065, 6.00726227594673864385067167688, 7.15338235857431075096387108974, 7.24873510617453755225057715176, 7.58921476107187061140994872605

Graph of the $Z$-function along the critical line