↑

Properties

Label 4-12e4-1.1-c1e2-0-15
Degree $4$
Conductor $20736$
Sign $1$
Analytic cond. $1.32214$
Root an. cond. $1.07230$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Related objects

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 8·7-s + 4·13-s − 16·19-s − 10·25-s + 8·31-s − 20·37-s − 16·43-s + 34·49-s + 28·61-s + 32·67-s − 20·73-s + 8·79-s + 32·91-s + 28·97-s − 40·103-s + 4·109-s − 22·121-s + 127-s + 131-s − 128·133-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + ⋯
L(s)  = 1  + 3.02·7-s + 1.10·13-s − 3.67·19-s − 2·25-s + 1.43·31-s − 3.28·37-s − 2.43·43-s + 34/7·49-s + 3.58·61-s + 3.90·67-s − 2.34·73-s + 0.900·79-s + 3.35·91-s + 2.84·97-s − 3.94·103-s + 0.383·109-s − 2·121-s + 0.0887·127-s + 0.0873·131-s − 11.0·133-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 20736 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 20736 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(20736\)    =    \(2^{8} \cdot 3^{4}\)
Sign: $1$
Analytic conductor: \(1.32214\)
Root analytic conductor: \(1.07230\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 20736,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(1.474585992\)
\(L(\frac12)\) \(\approx\) \(1.474585992\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
3 \( 1 \)
good5$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.5.a_k
7$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.7.ai_be
11$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.11.a_w
13$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.13.ae_be
17$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.17.a_bi
19$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.19.q_dy
23$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.23.a_bu
29$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.29.a_cg
31$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.31.ai_da
37$C_2$ \( ( 1 + 10 T + p T^{2} )^{2} \) 2.37.u_gs
41$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.41.a_de
43$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.43.q_fu
47$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.47.a_dq
53$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.53.a_ec
59$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.59.a_eo
61$C_2$ \( ( 1 - 14 T + p T^{2} )^{2} \) 2.61.abc_mg
67$C_2$ \( ( 1 - 16 T + p T^{2} )^{2} \) 2.67.abg_pa
71$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.71.a_fm
73$C_2$ \( ( 1 + 10 T + p T^{2} )^{2} \) 2.73.u_jm
79$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.79.ai_gs
83$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.83.a_gk
89$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.89.a_gw
97$C_2$ \( ( 1 - 14 T + p T^{2} )^{2} \) 2.97.abc_pa
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

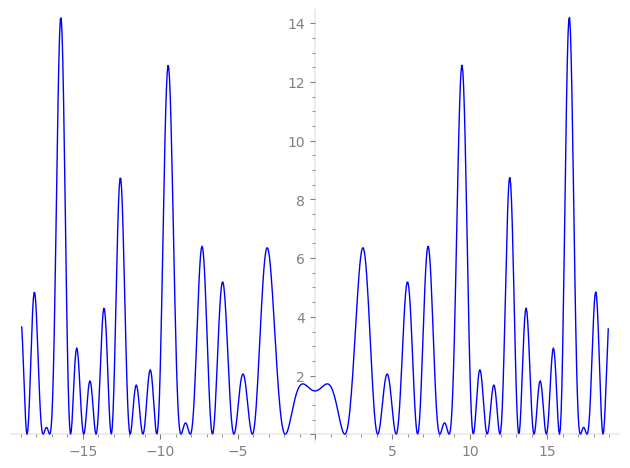
Imaginary part of the first few zeros on the critical line

−15.79487777633048798084752051242, −14.94637601970120006145797521849, −14.94637601970120006145797521849, −14.14961250099870306907964598019, −14.14961250099870306907964598019, −13.16759329932274946491561130296, −13.16759329932274946491561130296, −11.94687294246884746693957837802, −11.94687294246884746693957837802, −11.12315991811672295662035767470, −11.12315991811672295662035767470, −10.22525649903538281666764318697, −10.22525649903538281666764318697, −8.662053039688615672125838925077, −8.662053039688615672125838925077, −8.061333242868226986239179539676, −8.061333242868226986239179539676, −6.62696738834082263668854358565, −6.62696738834082263668854358565, −5.24060664699283394077045448716, −5.24060664699283394077045448716, −4.05061428132231144121252913355, −4.05061428132231144121252913355, −1.92209901273574427656973400179, −1.92209901273574427656973400179, 1.92209901273574427656973400179, 1.92209901273574427656973400179, 4.05061428132231144121252913355, 4.05061428132231144121252913355, 5.24060664699283394077045448716, 5.24060664699283394077045448716, 6.62696738834082263668854358565, 6.62696738834082263668854358565, 8.061333242868226986239179539676, 8.061333242868226986239179539676, 8.662053039688615672125838925077, 8.662053039688615672125838925077, 10.22525649903538281666764318697, 10.22525649903538281666764318697, 11.12315991811672295662035767470, 11.12315991811672295662035767470, 11.94687294246884746693957837802, 11.94687294246884746693957837802, 13.16759329932274946491561130296, 13.16759329932274946491561130296, 14.14961250099870306907964598019, 14.14961250099870306907964598019, 14.94637601970120006145797521849, 14.94637601970120006145797521849, 15.79487777633048798084752051242

Graph of the $Z$-function along the critical line