↑

Properties

Label 4-1184e2-1.1-c1e2-0-10
Degree $4$
Conductor $1401856$
Sign $1$
Analytic cond. $89.3835$
Root an. cond. $3.07478$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $2$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

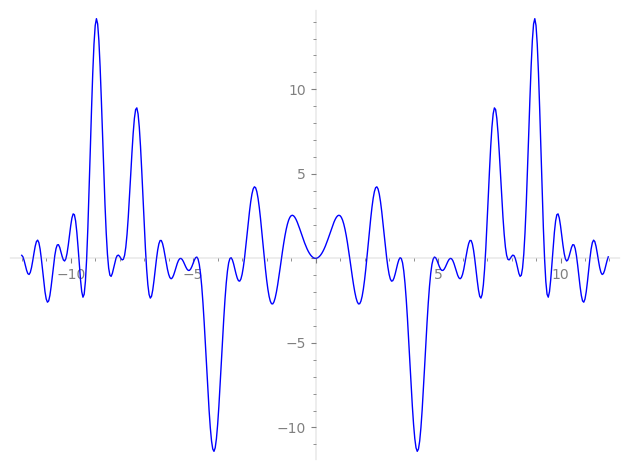
L(s)  = 1  − 2·3-s − 3·9-s − 6·11-s + 12·17-s − 4·19-s − 10·25-s + 14·27-s + 12·33-s − 18·41-s − 16·43-s − 13·49-s − 24·51-s + 8·57-s − 24·59-s + 8·67-s + 22·73-s + 20·75-s − 4·81-s − 18·83-s + 12·89-s + 16·97-s + 18·99-s − 24·107-s − 12·113-s + 5·121-s + 36·123-s + 127-s + ⋯
L(s)  = 1  − 1.15·3-s − 9-s − 1.80·11-s + 2.91·17-s − 0.917·19-s − 2·25-s + 2.69·27-s + 2.08·33-s − 2.81·41-s − 2.43·43-s − 1.85·49-s − 3.36·51-s + 1.05·57-s − 3.12·59-s + 0.977·67-s + 2.57·73-s + 2.30·75-s − 4/9·81-s − 1.97·83-s + 1.27·89-s + 1.62·97-s + 1.80·99-s − 2.32·107-s − 1.12·113-s + 5/11·121-s + 3.24·123-s + 0.0887·127-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1401856 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1401856 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(1401856\)    =    \(2^{10} \cdot 37^{2}\)
Sign: $1$
Analytic conductor: \(89.3835\)
Root analytic conductor: \(3.07478\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(2\)
Selberg data: \((4,\ 1401856,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
37$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
good3$C_2$ \( ( 1 + T + p T^{2} )^{2} \) 2.3.c_h
5$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.5.a_k
7$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.7.a_n
11$C_2$ \( ( 1 + 3 T + p T^{2} )^{2} \) 2.11.g_bf
13$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.13.a_k
17$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.17.am_cs
19$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.19.e_bq
23$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.23.a_k
29$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.29.a_w
31$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.31.a_bu
41$C_2$ \( ( 1 + 9 T + p T^{2} )^{2} \) 2.41.s_gh
43$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.43.q_fu
47$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.47.a_dh
53$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.53.a_dt
59$C_2$ \( ( 1 + 12 T + p T^{2} )^{2} \) 2.59.y_kc
61$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.61.a_cg
67$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.67.ai_fu
71$C_2$ \( ( 1 - 15 T + p T^{2} )( 1 + 15 T + p T^{2} ) \) 2.71.a_adf
73$C_2$ \( ( 1 - 11 T + p T^{2} )^{2} \) 2.73.aw_kh
79$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.79.a_cg
83$C_2$ \( ( 1 + 9 T + p T^{2} )^{2} \) 2.83.s_jn
89$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.89.am_ig
97$C_2$ \( ( 1 - 8 T + p T^{2} )^{2} \) 2.97.aq_jy
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−7.83252666101026187146437096539, −6.92702526110685059626904983928, −6.49509806030834552919855622210, −6.13026790010533892031415629049, −5.52397436821147602871559735263, −5.50302825732666851289149768404, −4.91803715229452696224797784043, −4.81124860316907390767416903100, −3.49656973901712201010716232454, −3.42634561262787911027610453075, −2.90414738025441870892963779928, −2.09291945273234411794912146252, −1.39370194281586028856128276808, 0, 0, 1.39370194281586028856128276808, 2.09291945273234411794912146252, 2.90414738025441870892963779928, 3.42634561262787911027610453075, 3.49656973901712201010716232454, 4.81124860316907390767416903100, 4.91803715229452696224797784043, 5.50302825732666851289149768404, 5.52397436821147602871559735263, 6.13026790010533892031415629049, 6.49509806030834552919855622210, 6.92702526110685059626904983928, 7.83252666101026187146437096539

Graph of the $Z$-function along the critical line