↑

Properties

Label 4-1630475-1.1-c1e2-0-7
Degree $4$
Conductor $1630475$
Sign $-1$
Analytic cond. $103.960$
Root an. cond. $3.19313$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $1$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 3·4-s + 2·5-s − 2·9-s − 11-s + 5·16-s + 6·20-s − 25-s − 20·31-s − 6·36-s − 3·44-s − 4·45-s − 49-s − 2·55-s + 4·59-s + 3·64-s − 24·71-s + 10·80-s − 5·81-s + 12·89-s + 2·99-s − 3·100-s + 121-s − 60·124-s − 12·125-s + 127-s + 131-s + 137-s + ⋯
L(s)  = 1  + 3/2·4-s + 0.894·5-s − 2/3·9-s − 0.301·11-s + 5/4·16-s + 1.34·20-s − 1/5·25-s − 3.59·31-s − 36-s − 0.452·44-s − 0.596·45-s − 1/7·49-s − 0.269·55-s + 0.520·59-s + 3/8·64-s − 2.84·71-s + 1.11·80-s − 5/9·81-s + 1.27·89-s + 0.201·99-s − 0.299·100-s + 1/11·121-s − 5.38·124-s − 1.07·125-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1630475 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1630475 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(1630475\)    =    \(5^{2} \cdot 7^{2} \cdot 11^{3}\)
Sign: $-1$
Analytic conductor: \(103.960\)
Root analytic conductor: \(3.19313\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 1630475,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad5$C_2$ \( 1 - 2 T + p T^{2} \)
7$C_2$ \( 1 + T^{2} \)
11$C_1$ \( 1 + T \)
good2$C_2^2$ \( 1 - 3 T^{2} + p^{2} T^{4} \) 2.2.a_ad
3$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.3.a_c
13$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.13.a_ak
17$C_2^2$ \( 1 - 18 T^{2} + p^{2} T^{4} \) 2.17.a_as
19$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.19.a_bm
23$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.23.a_be
29$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.29.a_w
31$C_2$ \( ( 1 + 10 T + p T^{2} )^{2} \) 2.31.u_gg
37$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.37.a_bm
41$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.41.a_co
43$C_2^2$ \( 1 + 58 T^{2} + p^{2} T^{4} \) 2.43.a_cg
47$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.47.a_ag
53$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.53.a_cs
59$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.59.ae_es
61$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.61.a_es
67$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.67.a_cs
71$C_2$ \( ( 1 + 12 T + p T^{2} )^{2} \) 2.71.y_la
73$C_2^2$ \( 1 - 82 T^{2} + p^{2} T^{4} \) 2.73.a_ade
79$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.79.a_dq
83$C_2$ \( ( 1 - p T^{2} )^{2} \) 2.83.a_agk
89$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.89.am_ig
97$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.97.a_dq
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

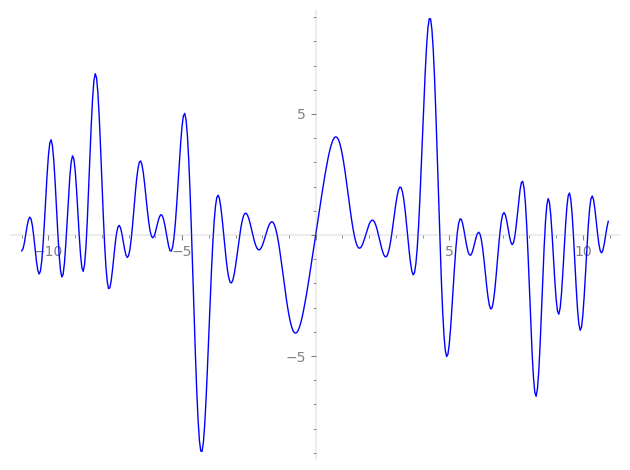
Imaginary part of the first few zeros on the critical line

−7.46127747363326771157161669823, −7.24266733214459675987556450307, −6.88644111010535416927201052141, −6.16131703698560659490677273092, −6.02967715717589461724363247324, −5.58013881532135247113220009754, −5.29120274672565051648185432644, −4.64426426210579357808086462080, −3.83193092345248498267473755969, −3.44033370812212446843781041764, −2.84156206421301966506253420212, −2.35165194264530572320119772609, −1.87025015711116528356850388928, −1.44183540096122748448332102848, 0, 1.44183540096122748448332102848, 1.87025015711116528356850388928, 2.35165194264530572320119772609, 2.84156206421301966506253420212, 3.44033370812212446843781041764, 3.83193092345248498267473755969, 4.64426426210579357808086462080, 5.29120274672565051648185432644, 5.58013881532135247113220009754, 6.02967715717589461724363247324, 6.16131703698560659490677273092, 6.88644111010535416927201052141, 7.24266733214459675987556450307, 7.46127747363326771157161669823

Graph of the $Z$-function along the critical line