↑

Properties

Label 4-4080e2-1.1-c1e2-0-17
Degree $4$
Conductor $16646400$
Sign $1$
Analytic cond. $1061.38$
Root an. cond. $5.70779$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 4·5-s − 9-s + 4·11-s + 8·19-s + 11·25-s + 8·31-s + 24·41-s + 4·45-s − 2·49-s − 16·55-s + 16·59-s − 12·61-s + 12·71-s + 81-s − 4·89-s − 32·95-s − 4·99-s − 28·101-s − 4·109-s − 10·121-s − 24·125-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + ⋯
L(s)  = 1  − 1.78·5-s − 1/3·9-s + 1.20·11-s + 1.83·19-s + 11/5·25-s + 1.43·31-s + 3.74·41-s + 0.596·45-s − 2/7·49-s − 2.15·55-s + 2.08·59-s − 1.53·61-s + 1.42·71-s + 1/9·81-s − 0.423·89-s − 3.28·95-s − 0.402·99-s − 2.78·101-s − 0.383·109-s − 0.909·121-s − 2.14·125-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 16646400 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 16646400 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(16646400\)    =    \(2^{8} \cdot 3^{2} \cdot 5^{2} \cdot 17^{2}\)
Sign: $1$
Analytic conductor: \(1061.38\)
Root analytic conductor: \(5.70779\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 16646400,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(2.432938557\)
\(L(\frac12)\) \(\approx\) \(2.432938557\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
3$C_2$ \( 1 + T^{2} \)
5$C_2$ \( 1 + 4 T + p T^{2} \)
17$C_2$ \( 1 + T^{2} \)
good7$C_2^2$ \( 1 + 2 T^{2} + p^{2} T^{4} \) 2.7.a_c
11$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.11.ae_ba
13$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.13.a_ak
19$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.19.ai_cc
23$C_2^2$ \( 1 + 18 T^{2} + p^{2} T^{4} \) 2.23.a_s
29$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.29.a_cg
31$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.31.ai_da
37$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.37.a_acs
41$C_2$ \( ( 1 - 12 T + p T^{2} )^{2} \) 2.41.ay_is
43$C_2^2$ \( 1 - 82 T^{2} + p^{2} T^{4} \) 2.43.a_ade
47$C_2^2$ \( 1 - 30 T^{2} + p^{2} T^{4} \) 2.47.a_abe
53$C_2^2$ \( 1 - 6 T^{2} + p^{2} T^{4} \) 2.53.a_ag
59$C_2$ \( ( 1 - 8 T + p T^{2} )^{2} \) 2.59.aq_ha
61$C_2$ \( ( 1 + 6 T + p T^{2} )^{2} \) 2.61.m_gc
67$C_2^2$ \( 1 - 130 T^{2} + p^{2} T^{4} \) 2.67.a_afa
71$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.71.am_gw
73$C_2^2$ \( 1 - 46 T^{2} + p^{2} T^{4} \) 2.73.a_abu
79$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.79.a_gc
83$C_2^2$ \( 1 - 22 T^{2} + p^{2} T^{4} \) 2.83.a_aw
89$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.89.e_ha
97$C_2^2$ \( 1 - 190 T^{2} + p^{2} T^{4} \) 2.97.a_ahi
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

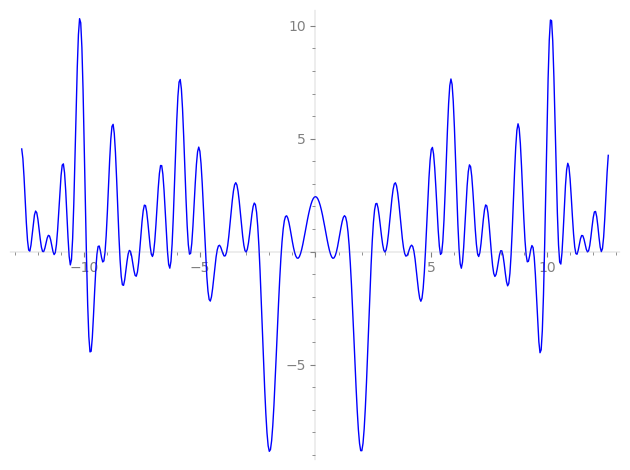
Imaginary part of the first few zeros on the critical line

−8.462808182337799826188212198933, −8.068533126986762954563082532788, −7.990489740249612775102926687536, −7.60009987487253453256230164403, −7.11369666345635162216653129497, −6.99134300920133697538578063421, −6.39414771413872667732740926626, −6.21309329378089135048557837031, −5.46440141782869406891558440944, −5.38135267244350226782944300168, −4.75436910847216724153881840279, −4.25879458342489762826589755189, −4.02824024102348416605273542499, −3.83648821186868112873701267090, −3.02854856610069554883216608885, −2.97791727399200541553666176952, −2.43191607744532336651517350463, −1.47513925195352867086416602885, −0.908752893182709857377028195202, −0.61848552766153890655358396386, 0.61848552766153890655358396386, 0.908752893182709857377028195202, 1.47513925195352867086416602885, 2.43191607744532336651517350463, 2.97791727399200541553666176952, 3.02854856610069554883216608885, 3.83648821186868112873701267090, 4.02824024102348416605273542499, 4.25879458342489762826589755189, 4.75436910847216724153881840279, 5.38135267244350226782944300168, 5.46440141782869406891558440944, 6.21309329378089135048557837031, 6.39414771413872667732740926626, 6.99134300920133697538578063421, 7.11369666345635162216653129497, 7.60009987487253453256230164403, 7.990489740249612775102926687536, 8.068533126986762954563082532788, 8.462808182337799826188212198933

Graph of the $Z$-function along the critical line