↑

Properties

Label 4-1512e2-1.1-c1e2-0-7
Degree $4$
Conductor $2286144$
Sign $1$
Analytic cond. $145.766$
Root an. cond. $3.47467$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

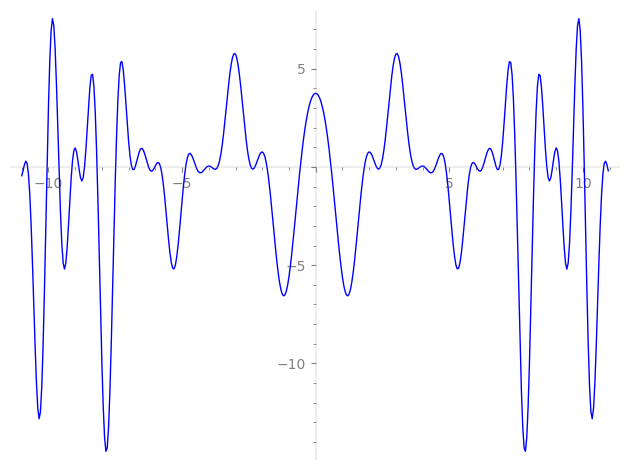
L(s)  = 1  + 2·2-s + 2·4-s + 8·11-s − 4·16-s − 6·17-s − 16·19-s + 16·22-s − 9·25-s − 8·32-s − 12·34-s − 32·38-s − 2·41-s + 22·43-s + 16·44-s + 49-s − 18·50-s + 30·59-s − 8·64-s − 16·67-s − 12·68-s + 12·73-s − 32·76-s − 4·82-s + 18·83-s + 44·86-s − 4·89-s + 24·97-s + ⋯
L(s)  = 1  + 1.41·2-s + 4-s + 2.41·11-s − 16-s − 1.45·17-s − 3.67·19-s + 3.41·22-s − 9/5·25-s − 1.41·32-s − 2.05·34-s − 5.19·38-s − 0.312·41-s + 3.35·43-s + 2.41·44-s + 1/7·49-s − 2.54·50-s + 3.90·59-s − 64-s − 1.95·67-s − 1.45·68-s + 1.40·73-s − 3.67·76-s − 0.441·82-s + 1.97·83-s + 4.74·86-s − 0.423·89-s + 2.43·97-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2286144 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2286144 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(2286144\)    =    \(2^{6} \cdot 3^{6} \cdot 7^{2}\)
Sign: $1$
Analytic conductor: \(145.766\)
Root analytic conductor: \(3.47467\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 2286144,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(3.749539769\)
\(L(\frac12)\) \(\approx\) \(3.749539769\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_2$ \( 1 - p T + p T^{2} \)
3 \( 1 \)
7$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
good5$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.5.a_j
11$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.11.ai_bm
13$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.13.a_w
17$C_2$ \( ( 1 + 3 T + p T^{2} )^{2} \) 2.17.g_br
19$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.19.q_dy
23$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.23.a_k
29$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.29.a_bq
31$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.31.a_ba
37$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.37.a_cn
41$C_2$ \( ( 1 + T + p T^{2} )^{2} \) 2.41.c_df
43$C_2$ \( ( 1 - 11 T + p T^{2} )^{2} \) 2.43.aw_hz
47$C_2$ \( ( 1 - 9 T + p T^{2} )( 1 + 9 T + p T^{2} ) \) 2.47.a_n
53$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.53.a_cs
59$C_2$ \( ( 1 - 15 T + p T^{2} )^{2} \) 2.59.abe_nf
61$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.61.a_ec
67$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.67.q_hq
71$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.71.a_ac
73$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.73.am_ha
79$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.79.a_gb
83$C_2$ \( ( 1 - 9 T + p T^{2} )^{2} \) 2.83.as_jn
89$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.89.e_ha
97$C_2$ \( ( 1 - 12 T + p T^{2} )^{2} \) 2.97.ay_na
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−7.48567647413624171857757042501, −6.88269156268701838964660075905, −6.75587037635177377501803178294, −6.25471251304940803802164013919, −6.01925406730418521392618394119, −5.80367615341180307099149099534, −4.86590526026148497681960970818, −4.47876350133431263053789868481, −4.07880642685856416996116102140, −3.90517995805379232478125425669, −3.66825379634424345995122136345, −2.42236155159716987191201970387, −2.27626756480610038380642233968, −1.82200069852459429520296401514, −0.57619866634073869454692864291, 0.57619866634073869454692864291, 1.82200069852459429520296401514, 2.27626756480610038380642233968, 2.42236155159716987191201970387, 3.66825379634424345995122136345, 3.90517995805379232478125425669, 4.07880642685856416996116102140, 4.47876350133431263053789868481, 4.86590526026148497681960970818, 5.80367615341180307099149099534, 6.01925406730418521392618394119, 6.25471251304940803802164013919, 6.75587037635177377501803178294, 6.88269156268701838964660075905, 7.48567647413624171857757042501

Graph of the $Z$-function along the critical line