↑

Properties

Label 4-1184e2-1.1-c1e2-0-5
Degree $4$
Conductor $1401856$
Sign $-1$
Analytic cond. $89.3835$
Root an. cond. $3.07478$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $1$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2·3-s − 3·9-s − 2·11-s − 8·17-s + 16·19-s − 6·25-s − 14·27-s − 4·33-s + 14·41-s − 4·43-s − 13·49-s − 16·51-s + 32·57-s + 24·59-s + 14·73-s − 12·75-s − 4·81-s − 6·83-s − 24·89-s − 16·97-s + 6·99-s + 8·107-s + 4·113-s − 19·121-s + 28·123-s + 127-s − 8·129-s + ⋯
L(s)  = 1  + 1.15·3-s − 9-s − 0.603·11-s − 1.94·17-s + 3.67·19-s − 6/5·25-s − 2.69·27-s − 0.696·33-s + 2.18·41-s − 0.609·43-s − 1.85·49-s − 2.24·51-s + 4.23·57-s + 3.12·59-s + 1.63·73-s − 1.38·75-s − 4/9·81-s − 0.658·83-s − 2.54·89-s − 1.62·97-s + 0.603·99-s + 0.773·107-s + 0.376·113-s − 1.72·121-s + 2.52·123-s + 0.0887·127-s − 0.704·129-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1401856 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1401856 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(1401856\)    =    \(2^{10} \cdot 37^{2}\)
Sign: $-1$
Analytic conductor: \(89.3835\)
Root analytic conductor: \(3.07478\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 1401856,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
37$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
good3$C_2$ \( ( 1 - T + p T^{2} )^{2} \) 2.3.ac_h
5$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.5.a_g
7$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.7.a_n
11$C_2$ \( ( 1 + T + p T^{2} )^{2} \) 2.11.c_x
13$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.13.a_ak
17$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.17.i_by
19$C_2$ \( ( 1 - 8 T + p T^{2} )^{2} \) 2.19.aq_dy
23$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.23.a_k
29$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.29.a_cc
31$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.31.a_bu
41$C_2$ \( ( 1 - 7 T + p T^{2} )^{2} \) 2.41.ao_fb
43$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.43.e_dm
47$C_2$ \( ( 1 - 9 T + p T^{2} )( 1 + 9 T + p T^{2} ) \) 2.47.a_n
53$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.53.a_dt
59$C_2$ \( ( 1 - 12 T + p T^{2} )^{2} \) 2.59.ay_kc
61$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.61.a_ec
67$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.67.a_fe
71$C_2$ \( ( 1 - 7 T + p T^{2} )( 1 + 7 T + p T^{2} ) \) 2.71.a_dp
73$C_2$ \( ( 1 - 7 T + p T^{2} )^{2} \) 2.73.ao_hn
79$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.79.a_gc
83$C_2$ \( ( 1 + 3 T + p T^{2} )^{2} \) 2.83.g_gt
89$C_2$ \( ( 1 + 12 T + p T^{2} )^{2} \) 2.89.y_mk
97$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.97.q_jy
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

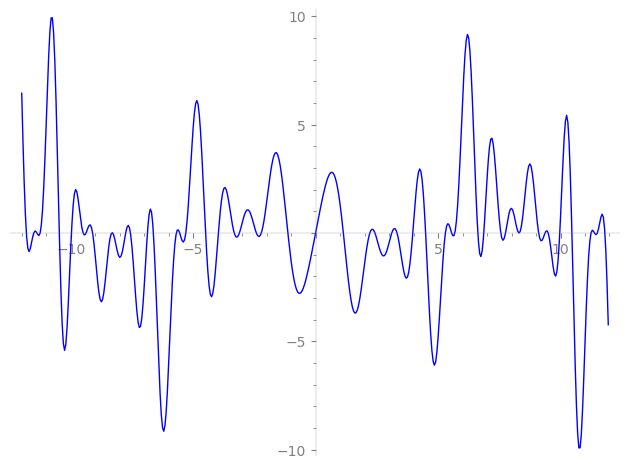
Imaginary part of the first few zeros on the critical line

−7.75456110220713984165022091972, −7.56200991672588442793948035593, −6.86682095955105512061953544939, −6.62515548141648090625940324832, −5.68536278134072713474064800006, −5.55163436815551852246094638061, −5.29977652365226555112580419353, −4.49161097993379934705251491217, −3.96828612768597928011477043556, −3.32391285921883791433244095783, −3.11027536009172942087782204014, −2.42130817560810783959503841896, −2.21589821767858410532420583902, −1.13230615835739562152636563080, 0, 1.13230615835739562152636563080, 2.21589821767858410532420583902, 2.42130817560810783959503841896, 3.11027536009172942087782204014, 3.32391285921883791433244095783, 3.96828612768597928011477043556, 4.49161097993379934705251491217, 5.29977652365226555112580419353, 5.55163436815551852246094638061, 5.68536278134072713474064800006, 6.62515548141648090625940324832, 6.86682095955105512061953544939, 7.56200991672588442793948035593, 7.75456110220713984165022091972

Graph of the $Z$-function along the critical line