↑

Properties

Label 4-453152-1.1-c1e2-0-10
Degree $4$
Conductor $453152$
Sign $-1$
Analytic cond. $28.8933$
Root an. cond. $2.31845$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $1$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2-s + 4-s + 4·5-s + 8-s − 6·9-s + 4·10-s − 4·13-s + 16-s + 2·17-s − 6·18-s + 4·20-s + 2·25-s − 4·26-s − 12·29-s + 32-s + 2·34-s − 6·36-s − 12·37-s + 4·40-s − 12·41-s − 24·45-s + 49-s + 2·50-s − 4·52-s − 4·53-s − 12·58-s + 4·61-s + ⋯
L(s)  = 1  + 0.707·2-s + 1/2·4-s + 1.78·5-s + 0.353·8-s − 2·9-s + 1.26·10-s − 1.10·13-s + 1/4·16-s + 0.485·17-s − 1.41·18-s + 0.894·20-s + 2/5·25-s − 0.784·26-s − 2.22·29-s + 0.176·32-s + 0.342·34-s − 36-s − 1.97·37-s + 0.632·40-s − 1.87·41-s − 3.57·45-s + 1/7·49-s + 0.282·50-s − 0.554·52-s − 0.549·53-s − 1.57·58-s + 0.512·61-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 453152 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 453152 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(453152\)    =    \(2^{5} \cdot 7^{2} \cdot 17^{2}\)
Sign: $-1$
Analytic conductor: \(28.8933\)
Root analytic conductor: \(2.31845\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 453152,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_1$ \( 1 - T \)
7$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
17$C_1$ \( ( 1 - T )^{2} \)
good3$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.3.a_g
5$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.5.ae_o
11$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.11.a_w
13$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.13.e_be
19$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.19.a_w
23$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.23.a_bu
29$C_2$ \( ( 1 + 6 T + p T^{2} )^{2} \) 2.29.m_dq
31$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.31.a_ck
37$C_2$ \( ( 1 + 6 T + p T^{2} )^{2} \) 2.37.m_eg
41$C_2$ \( ( 1 + 6 T + p T^{2} )^{2} \) 2.41.m_eo
43$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.43.a_acg
47$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.47.a_be
53$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.53.e_eg
59$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.59.a_dy
61$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.61.ae_ew
67$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.67.a_ak
71$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.71.a_fm
73$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.73.ae_fu
79$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.79.a_dq
83$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.83.a_w
89$C_2$ \( ( 1 - 10 T + p T^{2} )^{2} \) 2.89.au_ks
97$C_2$ \( ( 1 + 14 T + p T^{2} )^{2} \) 2.97.bc_pa
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

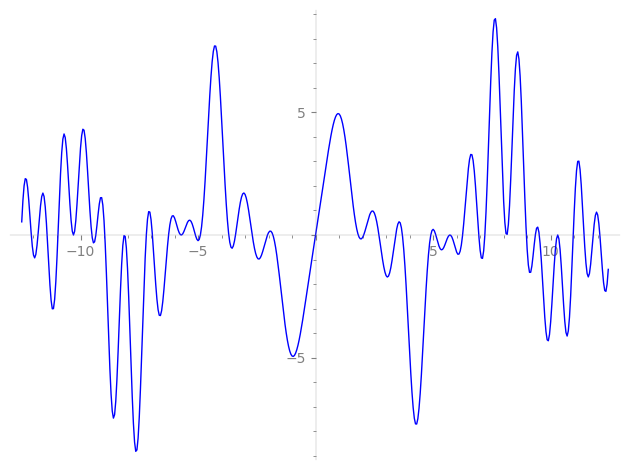
Imaginary part of the first few zeros on the critical line

−8.141215318250912713100120450381, −8.115728020271838283345679909969, −7.20010097624931167967073862090, −6.94219495068550059915873452189, −6.25342458965698612971884773553, −5.72806725976480398250034055565, −5.70286626752820956259075840901, −5.11332775341498038219899119581, −4.90031529950652941153483007995, −3.69220215237225216243720477255, −3.40674497567057131140915818833, −2.69561838868590084761774809099, −2.04650857588819893440526220286, −1.81489143388530531160395881484, 0, 1.81489143388530531160395881484, 2.04650857588819893440526220286, 2.69561838868590084761774809099, 3.40674497567057131140915818833, 3.69220215237225216243720477255, 4.90031529950652941153483007995, 5.11332775341498038219899119581, 5.70286626752820956259075840901, 5.72806725976480398250034055565, 6.25342458965698612971884773553, 6.94219495068550059915873452189, 7.20010097624931167967073862090, 8.115728020271838283345679909969, 8.141215318250912713100120450381

Graph of the $Z$-function along the critical line