↑

Properties

Label 4-2156e2-1.1-c1e2-0-7
Degree $4$
Conductor $4648336$
Sign $-1$
Analytic cond. $296.381$
Root an. cond. $4.14918$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $1$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

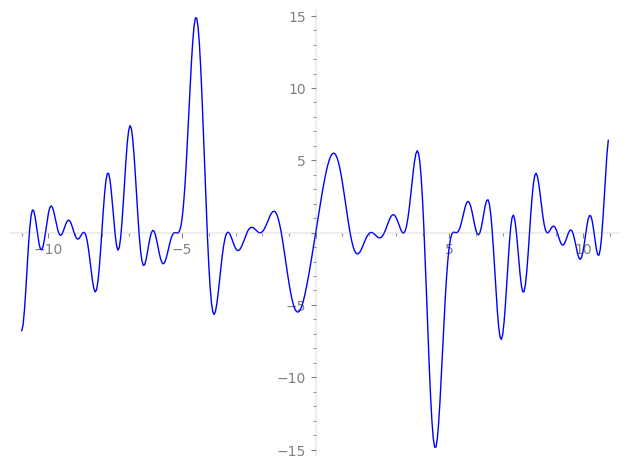
L(s)  = 1  + 2·3-s + 6·5-s − 3·9-s − 3·11-s + 12·15-s + 6·23-s + 17·25-s − 14·27-s − 14·31-s − 6·33-s − 2·37-s − 18·45-s − 18·47-s + 6·53-s − 18·55-s + 18·59-s − 14·67-s + 12·69-s + 34·75-s − 4·81-s + 30·89-s − 28·93-s − 20·97-s + 9·99-s + 22·103-s − 4·111-s + 12·113-s + ⋯
L(s)  = 1  + 1.15·3-s + 2.68·5-s − 9-s − 0.904·11-s + 3.09·15-s + 1.25·23-s + 17/5·25-s − 2.69·27-s − 2.51·31-s − 1.04·33-s − 0.328·37-s − 2.68·45-s − 2.62·47-s + 0.824·53-s − 2.42·55-s + 2.34·59-s − 1.71·67-s + 1.44·69-s + 3.92·75-s − 4/9·81-s + 3.17·89-s − 2.90·93-s − 2.03·97-s + 0.904·99-s + 2.16·103-s − 0.379·111-s + 1.12·113-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 4648336 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 4648336 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(4648336\)    =    \(2^{4} \cdot 7^{4} \cdot 11^{2}\)
Sign: $-1$
Analytic conductor: \(296.381\)
Root analytic conductor: \(4.14918\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 4648336,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
7 \( 1 \)
11$C_2$ \( 1 + 3 T + p T^{2} \)
good3$C_2$ \( ( 1 - T + p T^{2} )^{2} \) 2.3.ac_h
5$C_2$ \( ( 1 - 3 T + p T^{2} )^{2} \) 2.5.ag_t
13$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.13.a_w
17$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.17.a_z
19$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.19.a_bl
23$C_2$ \( ( 1 - 3 T + p T^{2} )^{2} \) 2.23.ag_cd
29$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.29.a_w
31$C_2$ \( ( 1 + 7 T + p T^{2} )^{2} \) 2.31.o_eh
37$C_2$ \( ( 1 + T + p T^{2} )^{2} \) 2.37.c_cx
41$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.41.a_bu
43$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.43.a_cs
47$C_2$ \( ( 1 + 9 T + p T^{2} )^{2} \) 2.47.s_gt
53$C_2$ \( ( 1 - 3 T + p T^{2} )^{2} \) 2.53.ag_el
59$C_2$ \( ( 1 - 9 T + p T^{2} )^{2} \) 2.59.as_hr
61$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.61.a_er
67$C_2$ \( ( 1 + 7 T + p T^{2} )^{2} \) 2.67.o_hb
71$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.71.a_fm
73$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.73.a_fp
79$C_2$ \( ( 1 - 13 T + p T^{2} )( 1 + 13 T + p T^{2} ) \) 2.79.a_al
83$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.83.a_w
89$C_2$ \( ( 1 - 15 T + p T^{2} )^{2} \) 2.89.abe_pn
97$C_2$ \( ( 1 + 10 T + p T^{2} )^{2} \) 2.97.u_li
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−7.27984610896713252075583450834, −6.61115025453772651831676615593, −6.14784187664657718195433732328, −6.02455306491682974275355684196, −5.28434328079604079625535316421, −5.24263093141446767528402808314, −5.13122282956772824311438407791, −4.05691268508438027952525861549, −3.31407617989174490462667281240, −3.24691773144996815761222106046, −2.57152545507023181505238705889, −2.11524838018749549647791443687, −2.04448974040096779312937543400, −1.28760101001418094464325191134, 0, 1.28760101001418094464325191134, 2.04448974040096779312937543400, 2.11524838018749549647791443687, 2.57152545507023181505238705889, 3.24691773144996815761222106046, 3.31407617989174490462667281240, 4.05691268508438027952525861549, 5.13122282956772824311438407791, 5.24263093141446767528402808314, 5.28434328079604079625535316421, 6.02455306491682974275355684196, 6.14784187664657718195433732328, 6.61115025453772651831676615593, 7.27984610896713252075583450834

Graph of the $Z$-function along the critical line