↑

Properties

Label 4-2720e2-1.1-c1e2-0-2
Degree $4$
Conductor $7398400$
Sign $1$
Analytic cond. $471.728$
Root an. cond. $4.66039$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

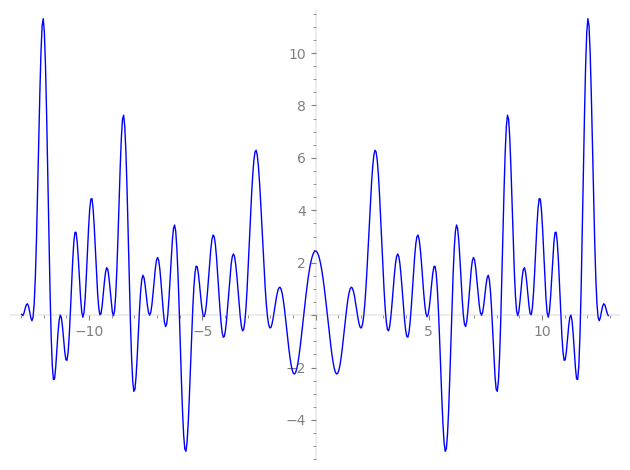
L(s)  = 1  + 5·9-s − 2·17-s + 8·23-s − 25-s − 18·31-s + 4·41-s − 6·47-s − 14·49-s − 6·71-s + 22·73-s − 16·79-s + 16·81-s + 18·89-s + 6·97-s + 16·103-s + 6·113-s + 18·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s − 10·153-s + 157-s + 163-s + 167-s + ⋯
L(s)  = 1  + 5/3·9-s − 0.485·17-s + 1.66·23-s − 1/5·25-s − 3.23·31-s + 0.624·41-s − 0.875·47-s − 2·49-s − 0.712·71-s + 2.57·73-s − 1.80·79-s + 16/9·81-s + 1.90·89-s + 0.609·97-s + 1.57·103-s + 0.564·113-s + 1.63·121-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s − 0.808·153-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 7398400 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 7398400 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(7398400\)    =    \(2^{10} \cdot 5^{2} \cdot 17^{2}\)
Sign: $1$
Analytic conductor: \(471.728\)
Root analytic conductor: \(4.66039\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 7398400,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(2.450737204\)
\(L(\frac12)\) \(\approx\) \(2.450737204\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
5$C_2$ \( 1 + T^{2} \)
17$C_1$ \( ( 1 + T )^{2} \)
good3$C_2^2$ \( 1 - 5 T^{2} + p^{2} T^{4} \) 2.3.a_af
7$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.7.a_o
11$C_2^2$ \( 1 - 18 T^{2} + p^{2} T^{4} \) 2.11.a_as
13$C_2^2$ \( 1 + 23 T^{2} + p^{2} T^{4} \) 2.13.a_x
19$C_2^2$ \( 1 + 11 T^{2} + p^{2} T^{4} \) 2.19.a_l
23$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.23.ai_ck
29$C_2^2$ \( 1 - 9 T^{2} + p^{2} T^{4} \) 2.29.a_aj
31$C_2$ \( ( 1 + 9 T + p T^{2} )^{2} \) 2.31.s_fn
37$C_2^2$ \( 1 - 38 T^{2} + p^{2} T^{4} \) 2.37.a_abm
41$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.41.ae_di
43$C_2^2$ \( 1 + 14 T^{2} + p^{2} T^{4} \) 2.43.a_o
47$C_2$ \( ( 1 + 3 T + p T^{2} )^{2} \) 2.47.g_dz
53$C_2^2$ \( 1 - 25 T^{2} + p^{2} T^{4} \) 2.53.a_az
59$C_2^2$ \( 1 - 37 T^{2} + p^{2} T^{4} \) 2.59.a_abl
61$C_2^2$ \( 1 - 121 T^{2} + p^{2} T^{4} \) 2.61.a_aer
67$C_2^2$ \( 1 - 70 T^{2} + p^{2} T^{4} \) 2.67.a_acs
71$C_2$ \( ( 1 + 3 T + p T^{2} )^{2} \) 2.71.g_fv
73$C_2$ \( ( 1 - 11 T + p T^{2} )^{2} \) 2.73.aw_kh
79$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.79.q_io
83$C_2^2$ \( 1 - 22 T^{2} + p^{2} T^{4} \) 2.83.a_aw
89$C_2$ \( ( 1 - 9 T + p T^{2} )^{2} \) 2.89.as_jz
97$C_2$ \( ( 1 - 3 T + p T^{2} )^{2} \) 2.97.ag_hv
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.944621350434959615591263331015, −8.908365419700544484129114934704, −8.183692890355370779934742926015, −7.78668781686018651416646761461, −7.33153340398582594922179037265, −7.32111507173789028749049300571, −6.70859969855580654523154540037, −6.52660317470314166122616974951, −6.01323302240018168665109945184, −5.43494525237759103717233504515, −4.96509426598907321956193315599, −4.88972634437902777351134835263, −4.20091742291819306109193994246, −3.91158182134311978715125473496, −3.33226378840405646559216960388, −3.09666320893612862514469280444, −2.13003096240094112475967479812, −1.85152636642657626779820415610, −1.34066626187505800036144011046, −0.52314186311900854171087295113, 0.52314186311900854171087295113, 1.34066626187505800036144011046, 1.85152636642657626779820415610, 2.13003096240094112475967479812, 3.09666320893612862514469280444, 3.33226378840405646559216960388, 3.91158182134311978715125473496, 4.20091742291819306109193994246, 4.88972634437902777351134835263, 4.96509426598907321956193315599, 5.43494525237759103717233504515, 6.01323302240018168665109945184, 6.52660317470314166122616974951, 6.70859969855580654523154540037, 7.32111507173789028749049300571, 7.33153340398582594922179037265, 7.78668781686018651416646761461, 8.183692890355370779934742926015, 8.908365419700544484129114934704, 8.944621350434959615591263331015

Graph of the $Z$-function along the critical line