↑

Properties

Label 4-623808-1.1-c1e2-0-43
Degree $4$
Conductor $623808$
Sign $1$
Analytic cond. $39.7745$
Root an. cond. $2.51131$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $0$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

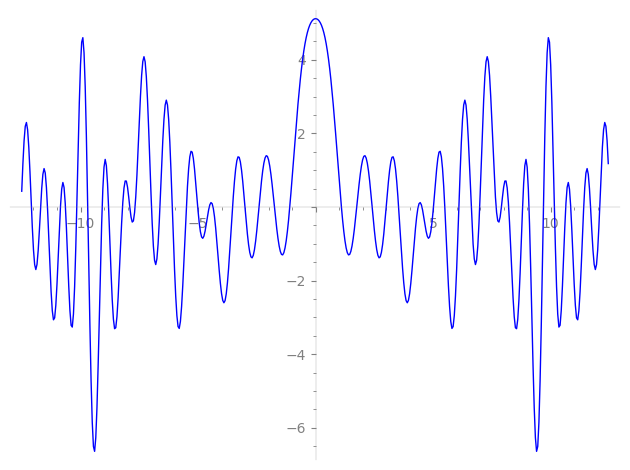
L(s)  = 1  + 2-s + 3-s + 4-s + 6-s + 4·7-s + 8-s + 9-s + 12-s + 4·14-s + 16-s + 18-s + 4·21-s + 24-s + 2·25-s + 27-s + 4·28-s + 8·29-s + 32-s + 36-s + 4·41-s + 4·42-s + 48-s + 2·49-s + 2·50-s − 8·53-s + 54-s + 4·56-s + ⋯
L(s)  = 1  + 0.707·2-s + 0.577·3-s + 1/2·4-s + 0.408·6-s + 1.51·7-s + 0.353·8-s + 1/3·9-s + 0.288·12-s + 1.06·14-s + 1/4·16-s + 0.235·18-s + 0.872·21-s + 0.204·24-s + 2/5·25-s + 0.192·27-s + 0.755·28-s + 1.48·29-s + 0.176·32-s + 1/6·36-s + 0.624·41-s + 0.617·42-s + 0.144·48-s + 2/7·49-s + 0.282·50-s − 1.09·53-s + 0.136·54-s + 0.534·56-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 623808 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 623808 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(623808\)    =    \(2^{6} \cdot 3^{3} \cdot 19^{2}\)
Sign: $1$
Analytic conductor: \(39.7745\)
Root analytic conductor: \(2.51131\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 623808,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(5.120570026\)
\(L(\frac12)\) \(\approx\) \(5.120570026\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_1$ \( 1 - T \)
3$C_1$ \( 1 - T \)
19$C_2$ \( 1 + p T^{2} \)
good5$C_2^2$ \( 1 - 2 T^{2} + p^{2} T^{4} \) 2.5.a_ac
7$C_2$$\times$$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + p T^{2} ) \) 2.7.ae_o
11$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.11.a_w
13$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.13.a_ak
17$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.17.a_ac
23$C_2^2$ \( 1 - 34 T^{2} + p^{2} T^{4} \) 2.23.a_abi
29$C_2$$\times$$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.29.ai_cs
31$C_2^2$ \( 1 - 34 T^{2} + p^{2} T^{4} \) 2.31.a_abi
37$C_2^2$ \( 1 - 10 T^{2} + p^{2} T^{4} \) 2.37.a_ak
41$C_2$$\times$$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.41.ae_cs
43$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.43.a_w
47$C_2^2$ \( 1 - 82 T^{2} + p^{2} T^{4} \) 2.47.a_ade
53$C_2$$\times$$C_2$ \( ( 1 + 2 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.53.i_eo
59$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.59.ai_fe
61$C_2$$\times$$C_2$ \( ( 1 + 2 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.61.m_fm
67$C_2^2$ \( 1 - 58 T^{2} + p^{2} T^{4} \) 2.67.a_acg
71$C_2$$\times$$C_2$ \( ( 1 - 16 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.71.ai_o
73$C_2$$\times$$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 14 T + p T^{2} ) \) 2.73.m_eo
79$C_2^2$ \( 1 - 66 T^{2} + p^{2} T^{4} \) 2.79.a_aco
83$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.83.a_dy
89$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.89.am_hq
97$C_2^2$ \( 1 - 162 T^{2} + p^{2} T^{4} \) 2.97.a_agg
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.213176759407349223846302287247, −7.903515134467079017839607534929, −7.67985780715341857454887866247, −6.97913361706962360137572896255, −6.62143874452648023979437937915, −6.09591432610903485406091342692, −5.49638547464841196078038222746, −5.01386340464067758455764263076, −4.52503456969604986414475524291, −4.36094897771292699704338322525, −3.53117369453153991020843668195, −3.00321613762990854888550128192, −2.40698180480353018569953253624, −1.74940504682165948024740002536, −1.09888824540654339078840468411, 1.09888824540654339078840468411, 1.74940504682165948024740002536, 2.40698180480353018569953253624, 3.00321613762990854888550128192, 3.53117369453153991020843668195, 4.36094897771292699704338322525, 4.52503456969604986414475524291, 5.01386340464067758455764263076, 5.49638547464841196078038222746, 6.09591432610903485406091342692, 6.62143874452648023979437937915, 6.97913361706962360137572896255, 7.67985780715341857454887866247, 7.903515134467079017839607534929, 8.213176759407349223846302287247

Graph of the $Z$-function along the critical line