| L(s) = 1 | − 3·3-s − 2·5-s − 2·7-s + 4·9-s − 5·11-s − 4·13-s + 6·15-s − 5·17-s − 19-s + 6·21-s − 4·23-s + 2·25-s − 6·27-s − 2·29-s − 14·31-s + 15·33-s + 4·35-s + 5·37-s + 12·39-s − 41-s − 43-s − 8·45-s + 10·47-s + 15·51-s + 4·53-s + 10·55-s + 3·57-s + ⋯ |
| L(s) = 1 | − 1.73·3-s − 0.894·5-s − 0.755·7-s + 4/3·9-s − 1.50·11-s − 1.10·13-s + 1.54·15-s − 1.21·17-s − 0.229·19-s + 1.30·21-s − 0.834·23-s + 2/5·25-s − 1.15·27-s − 0.371·29-s − 2.51·31-s + 2.61·33-s + 0.676·35-s + 0.821·37-s + 1.92·39-s − 0.156·41-s − 0.152·43-s − 1.19·45-s + 1.45·47-s + 2.10·51-s + 0.549·53-s + 1.34·55-s + 0.397·57-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 85280 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 85280 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
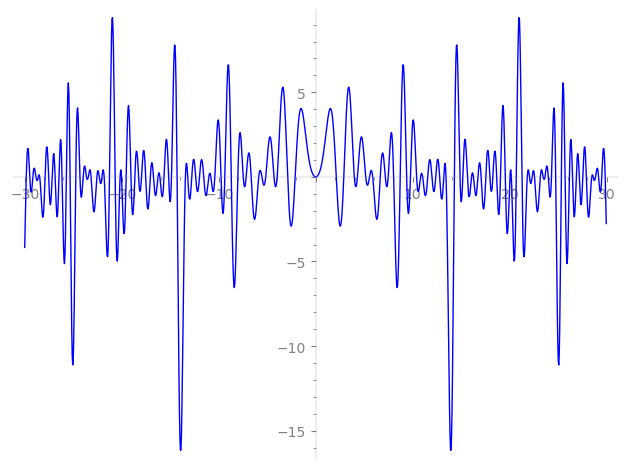
Imaginary part of the first few zeros on the critical line
−14.8674203095, −14.2906763893, −13.4336751911, −13.1961430689, −12.7768597857, −12.3722519320, −11.9820224469, −11.5439982771, −11.0225957597, −10.8106360816, −10.3987409333, −9.76095717204, −9.37035406688, −8.70626062509, −8.03148042778, −7.47177974025, −7.17214766692, −6.65166471530, −5.87394820759, −5.54377908567, −5.15379699824, −4.29881881046, −3.97656557291, −2.89306628083, −2.11814460777, 0, 0,
2.11814460777, 2.89306628083, 3.97656557291, 4.29881881046, 5.15379699824, 5.54377908567, 5.87394820759, 6.65166471530, 7.17214766692, 7.47177974025, 8.03148042778, 8.70626062509, 9.37035406688, 9.76095717204, 10.3987409333, 10.8106360816, 11.0225957597, 11.5439982771, 11.9820224469, 12.3722519320, 12.7768597857, 13.1961430689, 13.4336751911, 14.2906763893, 14.8674203095