↑

Properties

Label 4-792e2-1.1-c1e2-0-102
Degree $4$
Conductor $627264$
Sign $-1$
Analytic cond. $39.9948$
Root an. cond. $2.51478$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $1$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 2-s + 4-s − 8-s + 4·11-s + 16-s − 4·17-s − 4·22-s − 2·25-s + 8·29-s − 4·31-s − 32-s + 4·34-s − 4·37-s − 4·41-s + 4·44-s − 10·49-s + 2·50-s − 8·58-s + 4·62-s + 64-s − 16·67-s − 4·68-s + 4·74-s + 4·82-s − 8·83-s − 4·88-s − 12·97-s + ⋯
L(s)  = 1  − 0.707·2-s + 1/2·4-s − 0.353·8-s + 1.20·11-s + 1/4·16-s − 0.970·17-s − 0.852·22-s − 2/5·25-s + 1.48·29-s − 0.718·31-s − 0.176·32-s + 0.685·34-s − 0.657·37-s − 0.624·41-s + 0.603·44-s − 1.42·49-s + 0.282·50-s − 1.05·58-s + 0.508·62-s + 1/8·64-s − 1.95·67-s − 0.485·68-s + 0.464·74-s + 0.441·82-s − 0.878·83-s − 0.426·88-s − 1.21·97-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 627264 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 627264 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(627264\)    =    \(2^{6} \cdot 3^{4} \cdot 11^{2}\)
Sign: $-1$
Analytic conductor: \(39.9948\)
Root analytic conductor: \(2.51478\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 627264,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_1$ \( 1 + T \)
3 \( 1 \)
11$C_2$ \( 1 - 4 T + p T^{2} \)
good5$C_2^2$ \( 1 + 2 T^{2} + p^{2} T^{4} \) 2.5.a_c
7$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.7.a_k
13$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.13.a_ak
17$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.17.e_bm
19$C_2^2$ \( 1 - 14 T^{2} + p^{2} T^{4} \) 2.19.a_ao
23$C_2^2$ \( 1 - 2 T^{2} + p^{2} T^{4} \) 2.23.a_ac
29$C_2$$\times$$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.29.ai_cs
31$C_2$$\times$$C_2$ \( ( 1 + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.31.e_ck
37$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.37.e_da
41$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.41.e_di
43$C_2^2$ \( 1 - 30 T^{2} + p^{2} T^{4} \) 2.43.a_abe
47$C_2^2$ \( 1 + 14 T^{2} + p^{2} T^{4} \) 2.47.a_o
53$C_2^2$ \( 1 + 50 T^{2} + p^{2} T^{4} \) 2.53.a_by
59$C_2^2$ \( 1 - 10 T^{2} + p^{2} T^{4} \) 2.59.a_ak
61$C_2^2$ \( 1 + 70 T^{2} + p^{2} T^{4} \) 2.61.a_cs
67$C_2$$\times$$C_2$ \( ( 1 + 4 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.67.q_ha
71$C_2^2$ \( 1 - 66 T^{2} + p^{2} T^{4} \) 2.71.a_aco
73$C_2^2$ \( 1 - 82 T^{2} + p^{2} T^{4} \) 2.73.a_ade
79$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.79.a_es
83$C_2$$\times$$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 16 T + p T^{2} ) \) 2.83.i_bm
89$C_2^2$ \( 1 - 142 T^{2} + p^{2} T^{4} \) 2.89.a_afm
97$C_2$$\times$$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 14 T + p T^{2} ) \) 2.97.m_gk
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

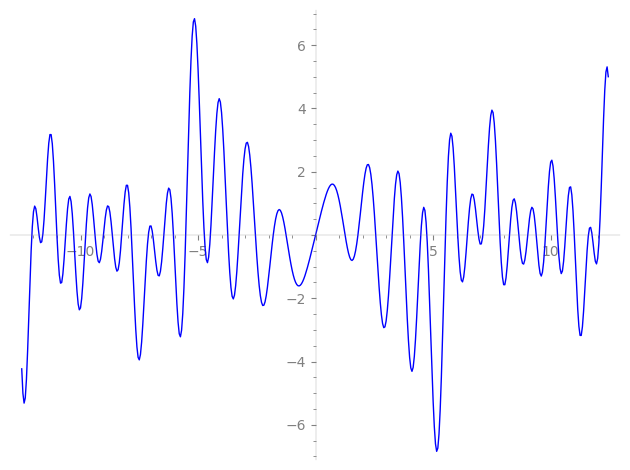
Imaginary part of the first few zeros on the critical line

−8.247546677414412379452316054223, −7.83559585441972008002539773015, −7.11436341230492644043971599477, −6.92489867476754446919607744684, −6.45580633785827035415011559528, −6.04637008437957373684957468214, −5.52473911372432491400298030079, −4.73381052597072891558853765596, −4.47418302487380259687564742910, −3.73781673727395107297505755240, −3.25410204939170867227324118178, −2.55999587436861408336452357208, −1.80095246466512907177948104322, −1.25447735745291973388640127652, 0, 1.25447735745291973388640127652, 1.80095246466512907177948104322, 2.55999587436861408336452357208, 3.25410204939170867227324118178, 3.73781673727395107297505755240, 4.47418302487380259687564742910, 4.73381052597072891558853765596, 5.52473911372432491400298030079, 6.04637008437957373684957468214, 6.45580633785827035415011559528, 6.92489867476754446919607744684, 7.11436341230492644043971599477, 7.83559585441972008002539773015, 8.247546677414412379452316054223

Graph of the $Z$-function along the critical line