↑

Properties

Label 4-4032e2-1.1-c1e2-0-27
Degree $4$
Conductor $16257024$
Sign $1$
Analytic cond. $1036.56$
Root an. cond. $5.67412$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $2$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

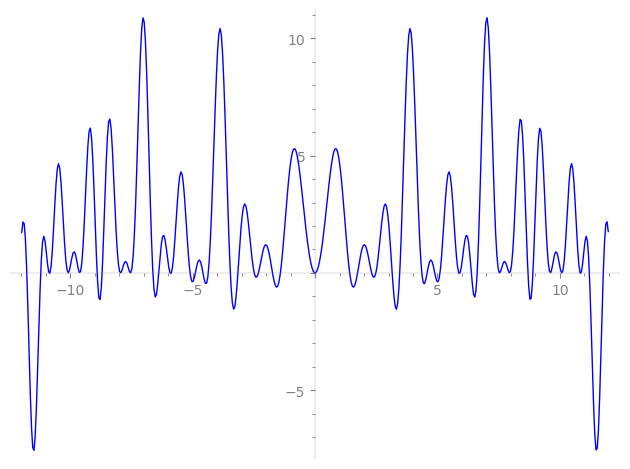
L(s)  = 1  + 2·5-s + 2·7-s − 4·11-s − 6·13-s − 2·19-s − 8·23-s − 2·25-s + 4·31-s + 4·35-s + 8·41-s − 4·43-s − 12·47-s + 3·49-s − 20·53-s − 8·55-s − 14·59-s − 18·61-s − 12·65-s − 8·67-s − 8·71-s + 12·73-s − 8·77-s + 8·79-s − 14·83-s + 12·89-s − 12·91-s − 4·95-s + ⋯
L(s)  = 1  + 0.894·5-s + 0.755·7-s − 1.20·11-s − 1.66·13-s − 0.458·19-s − 1.66·23-s − 2/5·25-s + 0.718·31-s + 0.676·35-s + 1.24·41-s − 0.609·43-s − 1.75·47-s + 3/7·49-s − 2.74·53-s − 1.07·55-s − 1.82·59-s − 2.30·61-s − 1.48·65-s − 0.977·67-s − 0.949·71-s + 1.40·73-s − 0.911·77-s + 0.900·79-s − 1.53·83-s + 1.27·89-s − 1.25·91-s − 0.410·95-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 16257024 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 16257024 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(16257024\)    =    \(2^{12} \cdot 3^{4} \cdot 7^{2}\)
Sign: $1$
Analytic conductor: \(1036.56\)
Root analytic conductor: \(5.67412\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(2\)
Selberg data: \((4,\ 16257024,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
3 \( 1 \)
7$C_1$ \( ( 1 - T )^{2} \)
good5$D_{4}$ \( 1 - 2 T + 6 T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.5.ac_g
11$C_4$ \( 1 + 4 T + 6 T^{2} + 4 p T^{3} + p^{2} T^{4} \) 2.11.e_g
13$D_{4}$ \( 1 + 6 T + 30 T^{2} + 6 p T^{3} + p^{2} T^{4} \) 2.13.g_be
17$C_2^2$ \( 1 + 14 T^{2} + p^{2} T^{4} \) 2.17.a_o
19$D_{4}$ \( 1 + 2 T + 34 T^{2} + 2 p T^{3} + p^{2} T^{4} \) 2.19.c_bi
23$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.23.i_ck
29$C_2^2$ \( 1 + 38 T^{2} + p^{2} T^{4} \) 2.29.a_bm
31$C_4$ \( 1 - 4 T + 46 T^{2} - 4 p T^{3} + p^{2} T^{4} \) 2.31.ae_bu
37$C_2^2$ \( 1 + 54 T^{2} + p^{2} T^{4} \) 2.37.a_cc
41$D_{4}$ \( 1 - 8 T + 78 T^{2} - 8 p T^{3} + p^{2} T^{4} \) 2.41.ai_da
43$D_{4}$ \( 1 + 4 T + 70 T^{2} + 4 p T^{3} + p^{2} T^{4} \) 2.43.e_cs
47$D_{4}$ \( 1 + 12 T + 110 T^{2} + 12 p T^{3} + p^{2} T^{4} \) 2.47.m_eg
53$C_2$ \( ( 1 + 10 T + p T^{2} )^{2} \) 2.53.u_hy
59$D_{4}$ \( 1 + 14 T + 162 T^{2} + 14 p T^{3} + p^{2} T^{4} \) 2.59.o_gg
61$D_{4}$ \( 1 + 18 T + 198 T^{2} + 18 p T^{3} + p^{2} T^{4} \) 2.61.s_hq
67$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.67.i_fu
71$D_{4}$ \( 1 + 8 T + 78 T^{2} + 8 p T^{3} + p^{2} T^{4} \) 2.71.i_da
73$D_{4}$ \( 1 - 12 T + 102 T^{2} - 12 p T^{3} + p^{2} T^{4} \) 2.73.am_dy
79$D_{4}$ \( 1 - 8 T + 94 T^{2} - 8 p T^{3} + p^{2} T^{4} \) 2.79.ai_dq
83$D_{4}$ \( 1 + 14 T + 210 T^{2} + 14 p T^{3} + p^{2} T^{4} \) 2.83.o_ic
89$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.89.am_ig
97$D_{4}$ \( 1 - 16 T + 238 T^{2} - 16 p T^{3} + p^{2} T^{4} \) 2.97.aq_je
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−7.943757221333397354202199069921, −7.940563827279596198148530255456, −7.54262144115475214564657783720, −7.53326932241791112376815230568, −6.62086825749603240306271901745, −6.38358407423723495699359777012, −5.92145618372123992021744740843, −5.86713511743146848773894653514, −5.10226636323751261448112923068, −4.88755832829268555178217164302, −4.57609327523921074151998906291, −4.35972553244539342656690799921, −3.45801405956865100209548083297, −3.14956405513278554719313963327, −2.48324751523398781163917704888, −2.31208576574067095957119909227, −1.73619235058518168362046950065, −1.41445032594151008781846420361, 0, 0, 1.41445032594151008781846420361, 1.73619235058518168362046950065, 2.31208576574067095957119909227, 2.48324751523398781163917704888, 3.14956405513278554719313963327, 3.45801405956865100209548083297, 4.35972553244539342656690799921, 4.57609327523921074151998906291, 4.88755832829268555178217164302, 5.10226636323751261448112923068, 5.86713511743146848773894653514, 5.92145618372123992021744740843, 6.38358407423723495699359777012, 6.62086825749603240306271901745, 7.53326932241791112376815230568, 7.54262144115475214564657783720, 7.940563827279596198148530255456, 7.943757221333397354202199069921

Graph of the $Z$-function along the critical line