↑

Properties

Label 4-2646e2-1.1-c1e2-0-39
Degree $4$
Conductor $7001316$
Sign $1$
Analytic cond. $446.409$
Root an. cond. $4.59656$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $2$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

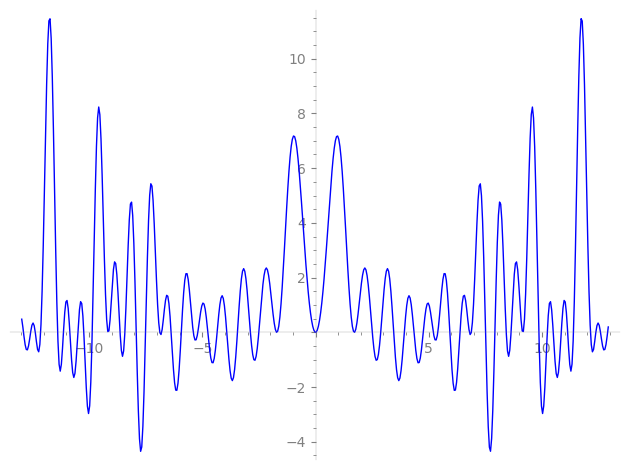
L(s)  = 1  + 2-s + 5-s − 8-s + 10-s − 2·11-s − 2·13-s − 16-s − 14·19-s − 2·22-s + 3·23-s + 5·25-s − 2·26-s − 8·29-s − 4·31-s − 12·37-s − 14·38-s − 40-s − 12·41-s + 8·43-s + 3·46-s − 8·47-s + 5·50-s − 8·53-s − 2·55-s − 8·58-s + 4·59-s − 13·61-s + ⋯
L(s)  = 1  + 0.707·2-s + 0.447·5-s − 0.353·8-s + 0.316·10-s − 0.603·11-s − 0.554·13-s − 1/4·16-s − 3.21·19-s − 0.426·22-s + 0.625·23-s + 25-s − 0.392·26-s − 1.48·29-s − 0.718·31-s − 1.97·37-s − 2.27·38-s − 0.158·40-s − 1.87·41-s + 1.21·43-s + 0.442·46-s − 1.16·47-s + 0.707·50-s − 1.09·53-s − 0.269·55-s − 1.05·58-s + 0.520·59-s − 1.66·61-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 7001316 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 7001316 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(7001316\)    =    \(2^{2} \cdot 3^{6} \cdot 7^{4}\)
Sign: $1$
Analytic conductor: \(446.409\)
Root analytic conductor: \(4.59656\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(2\)
Selberg data: \((4,\ 7001316,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_2$ \( 1 - T + T^{2} \)
3 \( 1 \)
7 \( 1 \)
good5$C_2^2$ \( 1 - T - 4 T^{2} - p T^{3} + p^{2} T^{4} \) 2.5.ab_ae
11$C_2^2$ \( 1 + 2 T - 7 T^{2} + 2 p T^{3} + p^{2} T^{4} \) 2.11.c_ah
13$C_2$ \( ( 1 - 5 T + p T^{2} )( 1 + 7 T + p T^{2} ) \) 2.13.c_aj
17$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.17.a_bi
19$C_2$ \( ( 1 + 7 T + p T^{2} )^{2} \) 2.19.o_dj
23$C_2^2$ \( 1 - 3 T - 14 T^{2} - 3 p T^{3} + p^{2} T^{4} \) 2.23.ad_ao
29$C_2^2$ \( 1 + 8 T + 35 T^{2} + 8 p T^{3} + p^{2} T^{4} \) 2.29.i_bj
31$C_2$ \( ( 1 - 7 T + p T^{2} )( 1 + 11 T + p T^{2} ) \) 2.31.e_ap
37$C_2$ \( ( 1 + 6 T + p T^{2} )^{2} \) 2.37.m_eg
41$C_2^2$ \( 1 + 12 T + 103 T^{2} + 12 p T^{3} + p^{2} T^{4} \) 2.41.m_dz
43$C_2$ \( ( 1 - 13 T + p T^{2} )( 1 + 5 T + p T^{2} ) \) 2.43.ai_v
47$C_2^2$ \( 1 + 8 T + 17 T^{2} + 8 p T^{3} + p^{2} T^{4} \) 2.47.i_r
53$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.53.i_es
59$C_2^2$ \( 1 - 4 T - 43 T^{2} - 4 p T^{3} + p^{2} T^{4} \) 2.59.ae_abr
61$C_2$ \( ( 1 - T + p T^{2} )( 1 + 14 T + p T^{2} ) \) 2.61.n_ee
67$C_2^2$ \( 1 - 2 T - 63 T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.67.ac_acl
71$C_2$ \( ( 1 - 5 T + p T^{2} )^{2} \) 2.71.ak_gl
73$C_2$ \( ( 1 + 14 T + p T^{2} )^{2} \) 2.73.bc_ne
79$C_2^2$ \( 1 - 11 T + 42 T^{2} - 11 p T^{3} + p^{2} T^{4} \) 2.79.al_bq
83$C_2^2$ \( 1 - 12 T + 61 T^{2} - 12 p T^{3} + p^{2} T^{4} \) 2.83.am_cj
89$C_2$ \( ( 1 + 14 T + p T^{2} )^{2} \) 2.89.bc_ok
97$C_2^2$ \( 1 - 2 T - 93 T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.97.ac_adp
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.632339367305196184732593963876, −8.420679483402568205018401144562, −7.918391762077813807299245896705, −7.50737071316690959530493670781, −6.87764194054143116205956771624, −6.79595314923919792670042746790, −6.37788466946222045803953153658, −5.92899531384411015140873258939, −5.39724301889777242303845425731, −5.19985936200252124144107672720, −4.75566634647335106699650992026, −4.34702921446122069556676595174, −3.91918896777548246665015648818, −3.44933026709040403705066430813, −2.87718553484940609256320982984, −2.50562984414926340719343611254, −1.72082807575796728045053229907, −1.70248342741047519259523539569, 0, 0, 1.70248342741047519259523539569, 1.72082807575796728045053229907, 2.50562984414926340719343611254, 2.87718553484940609256320982984, 3.44933026709040403705066430813, 3.91918896777548246665015648818, 4.34702921446122069556676595174, 4.75566634647335106699650992026, 5.19985936200252124144107672720, 5.39724301889777242303845425731, 5.92899531384411015140873258939, 6.37788466946222045803953153658, 6.79595314923919792670042746790, 6.87764194054143116205956771624, 7.50737071316690959530493670781, 7.918391762077813807299245896705, 8.420679483402568205018401144562, 8.632339367305196184732593963876

Graph of the $Z$-function along the critical line