↑

Properties

Label 4-194688-1.1-c1e2-0-11
Degree $4$
Conductor $194688$
Sign $-1$
Analytic cond. $12.4134$
Root an. cond. $1.87703$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $1$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 3·3-s + 6·9-s − 4·11-s + 2·13-s − 25-s − 9·27-s + 12·33-s + 2·37-s − 6·39-s − 2·47-s − 5·49-s + 4·59-s − 16·61-s + 2·71-s + 4·73-s + 3·75-s + 9·81-s + 24·83-s + 12·97-s − 24·99-s − 24·107-s − 14·109-s − 6·111-s + 12·117-s + 6·121-s + 127-s + 131-s + ⋯
L(s)  = 1  − 1.73·3-s + 2·9-s − 1.20·11-s + 0.554·13-s − 1/5·25-s − 1.73·27-s + 2.08·33-s + 0.328·37-s − 0.960·39-s − 0.291·47-s − 5/7·49-s + 0.520·59-s − 2.04·61-s + 0.237·71-s + 0.468·73-s + 0.346·75-s + 81-s + 2.63·83-s + 1.21·97-s − 2.41·99-s − 2.32·107-s − 1.34·109-s − 0.569·111-s + 1.10·117-s + 6/11·121-s + 0.0887·127-s + 0.0873·131-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 194688 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 194688 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(194688\)    =    \(2^{7} \cdot 3^{2} \cdot 13^{2}\)
Sign: $-1$
Analytic conductor: \(12.4134\)
Root analytic conductor: \(1.87703\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 194688,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
3$C_2$ \( 1 + p T + p T^{2} \)
13$C_1$ \( ( 1 - T )^{2} \)
good5$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.5.a_b
7$C_2$ \( ( 1 - 3 T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.7.a_f
11$C_2$$\times$$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.11.e_k
17$C_2^2$ \( 1 - 7 T^{2} + p^{2} T^{4} \) 2.17.a_ah
19$C_2^2$ \( 1 - 14 T^{2} + p^{2} T^{4} \) 2.19.a_ao
23$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.23.a_be
29$C_2^2$ \( 1 - 10 T^{2} + p^{2} T^{4} \) 2.29.a_ak
31$C_2^2$ \( 1 - 18 T^{2} + p^{2} T^{4} \) 2.31.a_as
37$C_2$$\times$$C_2$ \( ( 1 - 9 T + p T^{2} )( 1 + 7 T + p T^{2} ) \) 2.37.ac_l
41$C_2^2$ \( 1 + 50 T^{2} + p^{2} T^{4} \) 2.41.a_by
43$C_2^2$ \( 1 - 3 T^{2} + p^{2} T^{4} \) 2.43.a_ad
47$C_2$$\times$$C_2$ \( ( 1 - 7 T + p T^{2} )( 1 + 9 T + p T^{2} ) \) 2.47.c_bf
53$C_2^2$ \( 1 + 10 T^{2} + p^{2} T^{4} \) 2.53.a_k
59$C_2$$\times$$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.59.ae_ec
61$C_2$$\times$$C_2$ \( ( 1 + 4 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.61.q_go
67$C_2^2$ \( 1 - 46 T^{2} + p^{2} T^{4} \) 2.67.a_abu
71$C_2$$\times$$C_2$ \( ( 1 - 13 T + p T^{2} )( 1 + 11 T + p T^{2} ) \) 2.71.ac_ab
73$C_2$$\times$$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.73.ae_fe
79$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.79.a_fm
83$C_2$ \( ( 1 - 12 T + p T^{2} )^{2} \) 2.83.ay_ly
89$C_2^2$ \( 1 + 30 T^{2} + p^{2} T^{4} \) 2.89.a_be
97$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.97.am_ig
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

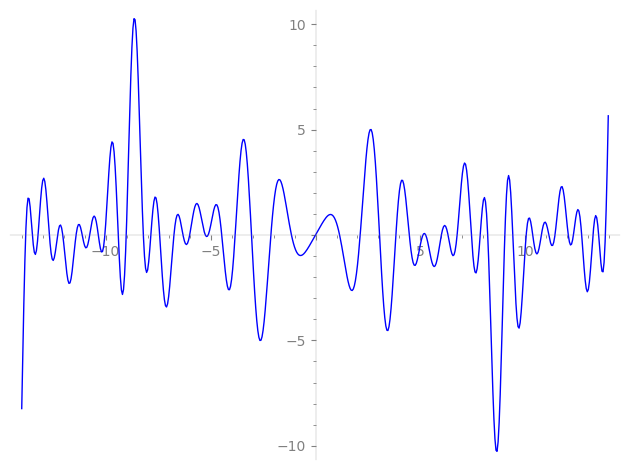
Imaginary part of the first few zeros on the critical line

−9.021179339698169784384036403055, −8.204524590098548683092760080407, −7.84713115092968817973809581066, −7.42772728546378356970089714645, −6.74683241206376404943690251380, −6.31394879855169309643898393272, −5.99692452132684010344841520792, −5.25078367049644905669734768768, −5.11733226063913190071078900940, −4.46886074650188144710158979308, −3.82994188950258817577735192270, −3.05038675572331186615313729926, −2.12789053642440238731445150527, −1.14655538396453240872812031707, 0, 1.14655538396453240872812031707, 2.12789053642440238731445150527, 3.05038675572331186615313729926, 3.82994188950258817577735192270, 4.46886074650188144710158979308, 5.11733226063913190071078900940, 5.25078367049644905669734768768, 5.99692452132684010344841520792, 6.31394879855169309643898393272, 6.74683241206376404943690251380, 7.42772728546378356970089714645, 7.84713115092968817973809581066, 8.204524590098548683092760080407, 9.021179339698169784384036403055

Graph of the $Z$-function along the critical line