| L(s) = 1 | + 2-s + 4-s + 2·5-s + 7-s + 8-s + 2·10-s + 13-s + 14-s + 16-s + 6·17-s − 2·19-s + 2·20-s − 4·23-s − 25-s + 26-s + 28-s + 6·29-s + 32-s + 6·34-s + 2·35-s − 4·37-s − 2·38-s + 2·40-s + 8·41-s − 2·43-s − 4·46-s − 4·47-s + ⋯ |
| L(s) = 1 | + 0.707·2-s + 1/2·4-s + 0.894·5-s + 0.377·7-s + 0.353·8-s + 0.632·10-s + 0.277·13-s + 0.267·14-s + 1/4·16-s + 1.45·17-s − 0.458·19-s + 0.447·20-s − 0.834·23-s − 1/5·25-s + 0.196·26-s + 0.188·28-s + 1.11·29-s + 0.176·32-s + 1.02·34-s + 0.338·35-s − 0.657·37-s − 0.324·38-s + 0.316·40-s + 1.24·41-s − 0.304·43-s − 0.589·46-s − 0.583·47-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 198198 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 198198 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 - T \) | |
| 3 | \( 1 \) | |
| 7 | \( 1 - T \) | |
| 11 | \( 1 \) | |
| 13 | \( 1 - T \) | |
| good | 5 | \( 1 - 2 T + p T^{2} \) | 1.5.ac |
| 17 | \( 1 - 6 T + p T^{2} \) | 1.17.ag |
| 19 | \( 1 + 2 T + p T^{2} \) | 1.19.c |
| 23 | \( 1 + 4 T + p T^{2} \) | 1.23.e |
| 29 | \( 1 - 6 T + p T^{2} \) | 1.29.ag |
| 31 | \( 1 + p T^{2} \) | 1.31.a |
| 37 | \( 1 + 4 T + p T^{2} \) | 1.37.e |
| 41 | \( 1 - 8 T + p T^{2} \) | 1.41.ai |
| 43 | \( 1 + 2 T + p T^{2} \) | 1.43.c |
| 47 | \( 1 + 4 T + p T^{2} \) | 1.47.e |
| 53 | \( 1 + 10 T + p T^{2} \) | 1.53.k |
| 59 | \( 1 + 4 T + p T^{2} \) | 1.59.e |
| 61 | \( 1 + 2 T + p T^{2} \) | 1.61.c |
| 67 | \( 1 + 12 T + p T^{2} \) | 1.67.m |
| 71 | \( 1 - 2 T + p T^{2} \) | 1.71.ac |
| 73 | \( 1 - 4 T + p T^{2} \) | 1.73.ae |
| 79 | \( 1 - 8 T + p T^{2} \) | 1.79.ai |
| 83 | \( 1 + 6 T + p T^{2} \) | 1.83.g |
| 89 | \( 1 + 14 T + p T^{2} \) | 1.89.o |
| 97 | \( 1 + 10 T + p T^{2} \) | 1.97.k |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
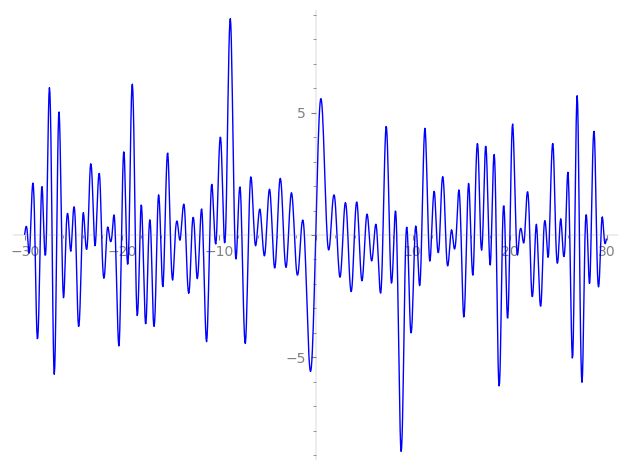
Imaginary part of the first few zeros on the critical line
−13.39357649149770, −12.78451099614515, −12.46915159285329, −11.94466018651499, −11.61263019669970, −10.92702557098101, −10.42598728757810, −10.22264598358758, −9.466455762746312, −9.299496636593411, −8.352902652401735, −8.068337821021410, −7.611165033145035, −6.928442772065132, −6.329108355265190, −6.042682848642521, −5.514169465523161, −5.092065903379153, −4.465722508911119, −3.985150125472594, −3.311471416615025, −2.809800227799195, −2.191961854790320, −1.527097236130979, −1.169273684033008, 0,
1.169273684033008, 1.527097236130979, 2.191961854790320, 2.809800227799195, 3.311471416615025, 3.985150125472594, 4.465722508911119, 5.092065903379153, 5.514169465523161, 6.042682848642521, 6.329108355265190, 6.928442772065132, 7.611165033145035, 8.068337821021410, 8.352902652401735, 9.299496636593411, 9.466455762746312, 10.22264598358758, 10.42598728757810, 10.92702557098101, 11.61263019669970, 11.94466018651499, 12.46915159285329, 12.78451099614515, 13.39357649149770