| L(s) = 1 | − 2-s + 2·3-s + 4-s − 2·6-s − 8-s + 9-s + 6·11-s + 2·12-s + 7·13-s + 16-s + 2·17-s − 18-s − 2·19-s − 6·22-s − 6·23-s − 2·24-s − 7·26-s − 4·27-s + 6·29-s − 9·31-s − 32-s + 12·33-s − 2·34-s + 36-s − 10·37-s + 2·38-s + 14·39-s + ⋯ |
| L(s) = 1 | − 0.707·2-s + 1.15·3-s + 1/2·4-s − 0.816·6-s − 0.353·8-s + 1/3·9-s + 1.80·11-s + 0.577·12-s + 1.94·13-s + 1/4·16-s + 0.485·17-s − 0.235·18-s − 0.458·19-s − 1.27·22-s − 1.25·23-s − 0.408·24-s − 1.37·26-s − 0.769·27-s + 1.11·29-s − 1.61·31-s − 0.176·32-s + 2.08·33-s − 0.342·34-s + 1/6·36-s − 1.64·37-s + 0.324·38-s + 2.24·39-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 193550 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 193550 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(4.095192014\) |
| \(L(\frac12)\) |
\(\approx\) |
\(4.095192014\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 + T \) | |
| 5 | \( 1 \) | |
| 7 | \( 1 \) | |
| 79 | \( 1 - T \) | |
| good | 3 | \( 1 - 2 T + p T^{2} \) | 1.3.ac |
| 11 | \( 1 - 6 T + p T^{2} \) | 1.11.ag |
| 13 | \( 1 - 7 T + p T^{2} \) | 1.13.ah |
| 17 | \( 1 - 2 T + p T^{2} \) | 1.17.ac |
| 19 | \( 1 + 2 T + p T^{2} \) | 1.19.c |
| 23 | \( 1 + 6 T + p T^{2} \) | 1.23.g |
| 29 | \( 1 - 6 T + p T^{2} \) | 1.29.ag |
| 31 | \( 1 + 9 T + p T^{2} \) | 1.31.j |
| 37 | \( 1 + 10 T + p T^{2} \) | 1.37.k |
| 41 | \( 1 - 6 T + p T^{2} \) | 1.41.ag |
| 43 | \( 1 + p T^{2} \) | 1.43.a |
| 47 | \( 1 + 7 T + p T^{2} \) | 1.47.h |
| 53 | \( 1 - 12 T + p T^{2} \) | 1.53.am |
| 59 | \( 1 + T + p T^{2} \) | 1.59.b |
| 61 | \( 1 - 11 T + p T^{2} \) | 1.61.al |
| 67 | \( 1 - 4 T + p T^{2} \) | 1.67.ae |
| 71 | \( 1 + 10 T + p T^{2} \) | 1.71.k |
| 73 | \( 1 - 14 T + p T^{2} \) | 1.73.ao |
| 83 | \( 1 + 4 T + p T^{2} \) | 1.83.e |
| 89 | \( 1 - T + p T^{2} \) | 1.89.ab |
| 97 | \( 1 - 6 T + p T^{2} \) | 1.97.ag |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
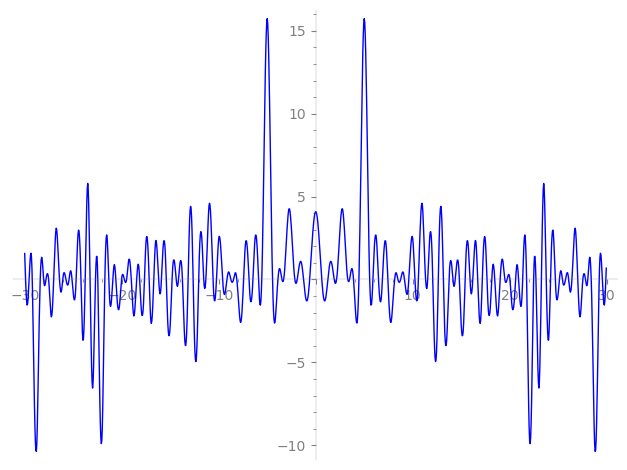
Imaginary part of the first few zeros on the critical line
−13.15411382698574, −12.63612909525264, −12.06559856201676, −11.54128658264779, −11.32047622915376, −10.58458747304694, −10.22978106995683, −9.598541176464774, −9.157213251555238, −8.752568600904498, −8.476237735145601, −8.127033006575294, −7.437301712653856, −6.876973261385175, −6.473537989521862, −5.894058415688349, −5.559995308300858, −4.454067270191978, −3.900948584417725, −3.485300720596778, −3.303420266065905, −2.151959532946927, −1.909027999490911, −1.251128710017004, −0.6256069772110350,
0.6256069772110350, 1.251128710017004, 1.909027999490911, 2.151959532946927, 3.303420266065905, 3.485300720596778, 3.900948584417725, 4.454067270191978, 5.559995308300858, 5.894058415688349, 6.473537989521862, 6.876973261385175, 7.437301712653856, 8.127033006575294, 8.476237735145601, 8.752568600904498, 9.157213251555238, 9.598541176464774, 10.22978106995683, 10.58458747304694, 11.32047622915376, 11.54128658264779, 12.06559856201676, 12.63612909525264, 13.15411382698574