| L(s) = 1 | − 2-s − 2·3-s + 4-s + 2·6-s − 8-s + 9-s − 2·11-s − 2·12-s + 13-s + 16-s − 2·17-s − 18-s − 6·19-s + 2·22-s + 2·23-s + 2·24-s − 26-s + 4·27-s + 6·29-s − 7·31-s − 32-s + 4·33-s + 2·34-s + 36-s + 6·37-s + 6·38-s − 2·39-s + ⋯ |
| L(s) = 1 | − 0.707·2-s − 1.15·3-s + 1/2·4-s + 0.816·6-s − 0.353·8-s + 1/3·9-s − 0.603·11-s − 0.577·12-s + 0.277·13-s + 1/4·16-s − 0.485·17-s − 0.235·18-s − 1.37·19-s + 0.426·22-s + 0.417·23-s + 0.408·24-s − 0.196·26-s + 0.769·27-s + 1.11·29-s − 1.25·31-s − 0.176·32-s + 0.696·33-s + 0.342·34-s + 1/6·36-s + 0.986·37-s + 0.973·38-s − 0.320·39-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 193550 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 193550 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 + T \) | |
| 5 | \( 1 \) | |
| 7 | \( 1 \) | |
| 79 | \( 1 - T \) | |
| good | 3 | \( 1 + 2 T + p T^{2} \) | 1.3.c |
| 11 | \( 1 + 2 T + p T^{2} \) | 1.11.c |
| 13 | \( 1 - T + p T^{2} \) | 1.13.ab |
| 17 | \( 1 + 2 T + p T^{2} \) | 1.17.c |
| 19 | \( 1 + 6 T + p T^{2} \) | 1.19.g |
| 23 | \( 1 - 2 T + p T^{2} \) | 1.23.ac |
| 29 | \( 1 - 6 T + p T^{2} \) | 1.29.ag |
| 31 | \( 1 + 7 T + p T^{2} \) | 1.31.h |
| 37 | \( 1 - 6 T + p T^{2} \) | 1.37.ag |
| 41 | \( 1 - 2 T + p T^{2} \) | 1.41.ac |
| 43 | \( 1 + 8 T + p T^{2} \) | 1.43.i |
| 47 | \( 1 - 3 T + p T^{2} \) | 1.47.ad |
| 53 | \( 1 - 4 T + p T^{2} \) | 1.53.ae |
| 59 | \( 1 + 11 T + p T^{2} \) | 1.59.l |
| 61 | \( 1 + 7 T + p T^{2} \) | 1.61.h |
| 67 | \( 1 - 4 T + p T^{2} \) | 1.67.ae |
| 71 | \( 1 - 6 T + p T^{2} \) | 1.71.ag |
| 73 | \( 1 + 6 T + p T^{2} \) | 1.73.g |
| 83 | \( 1 + 12 T + p T^{2} \) | 1.83.m |
| 89 | \( 1 - 15 T + p T^{2} \) | 1.89.ap |
| 97 | \( 1 + 6 T + p T^{2} \) | 1.97.g |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
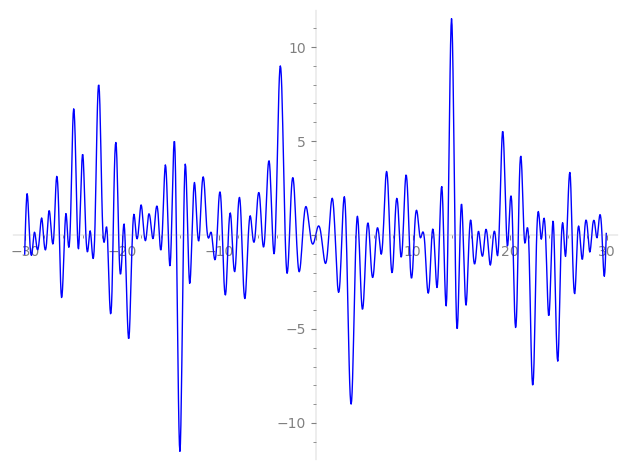
Imaginary part of the first few zeros on the critical line
−13.18997896431744, −12.75756976115251, −12.17813014725232, −11.97933057663917, −11.16604767808508, −10.93470181517817, −10.71237195132845, −10.16191192892899, −9.624062105680580, −9.000475728395481, −8.629469494269949, −8.115159990814358, −7.634819575534442, −6.948477418127445, −6.516313225613586, −6.237750481039997, −5.530772776110119, −5.234892019608423, −4.449251485772569, −4.158439031587596, −3.153137419237933, −2.703240320967884, −1.997584942979371, −1.348732785425058, −0.5609493322293974, 0,
0.5609493322293974, 1.348732785425058, 1.997584942979371, 2.703240320967884, 3.153137419237933, 4.158439031587596, 4.449251485772569, 5.234892019608423, 5.530772776110119, 6.237750481039997, 6.516313225613586, 6.948477418127445, 7.634819575534442, 8.115159990814358, 8.629469494269949, 9.000475728395481, 9.624062105680580, 10.16191192892899, 10.71237195132845, 10.93470181517817, 11.16604767808508, 11.97933057663917, 12.17813014725232, 12.75756976115251, 13.18997896431744