↑

Properties

Label 4-48e3-1.1-c1e2-0-18
Degree $4$
Conductor $110592$
Sign $-1$
Analytic cond. $7.05144$
Root an. cond. $1.62955$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $1$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 3-s + 9-s − 4·11-s − 8·13-s − 4·23-s − 2·25-s + 27-s − 4·33-s + 4·37-s − 8·39-s − 12·47-s + 10·49-s − 8·59-s − 4·61-s − 4·69-s − 4·71-s + 4·73-s − 2·75-s + 81-s − 4·83-s − 4·97-s − 4·99-s − 32·107-s + 4·111-s − 8·117-s − 6·121-s + 127-s + ⋯
L(s)  = 1  + 0.577·3-s + 1/3·9-s − 1.20·11-s − 2.21·13-s − 0.834·23-s − 2/5·25-s + 0.192·27-s − 0.696·33-s + 0.657·37-s − 1.28·39-s − 1.75·47-s + 10/7·49-s − 1.04·59-s − 0.512·61-s − 0.481·69-s − 0.474·71-s + 0.468·73-s − 0.230·75-s + 1/9·81-s − 0.439·83-s − 0.406·97-s − 0.402·99-s − 3.09·107-s + 0.379·111-s − 0.739·117-s − 0.545·121-s + 0.0887·127-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 110592 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 110592 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(110592\)    =    \(2^{12} \cdot 3^{3}\)
Sign: $-1$
Analytic conductor: \(7.05144\)
Root analytic conductor: \(1.62955\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(1\)
Selberg data: \((4,\ 110592,\ (\ :1/2, 1/2),\ -1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
3$C_1$ \( 1 - T \)
good5$C_2^2$ \( 1 + 2 T^{2} + p^{2} T^{4} \) 2.5.a_c
7$C_2^2$ \( 1 - 10 T^{2} + p^{2} T^{4} \) 2.7.a_ak
11$C_2$$\times$$C_2$ \( ( 1 + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.11.e_w
13$C_2$$\times$$C_2$ \( ( 1 + 2 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.13.i_bm
17$C_2^2$ \( 1 - 10 T^{2} + p^{2} T^{4} \) 2.17.a_ak
19$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.19.a_w
23$C_2$$\times$$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.23.e_o
29$C_2^2$ \( 1 + 10 T^{2} + p^{2} T^{4} \) 2.29.a_k
31$C_2^2$ \( 1 + 54 T^{2} + p^{2} T^{4} \) 2.31.a_cc
37$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.37.ae_o
41$C_2^2$ \( 1 - 42 T^{2} + p^{2} T^{4} \) 2.41.a_abq
43$C_2^2$ \( 1 - 42 T^{2} + p^{2} T^{4} \) 2.43.a_abq
47$C_2$$\times$$C_2$ \( ( 1 + 4 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.47.m_ew
53$C_2^2$ \( 1 - 6 T^{2} + p^{2} T^{4} \) 2.53.a_ag
59$C_2$$\times$$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.59.i_cs
61$C_2$$\times$$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.61.e_eg
67$C_2^2$ \( 1 - 58 T^{2} + p^{2} T^{4} \) 2.67.a_acg
71$C_2$$\times$$C_2$ \( ( 1 + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.71.e_fm
73$C_2$$\times$$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.73.ae_fe
79$C_2^2$ \( 1 - 10 T^{2} + p^{2} T^{4} \) 2.79.a_ak
83$C_2$$\times$$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 16 T + p T^{2} ) \) 2.83.e_aba
89$C_2^2$ \( 1 - 130 T^{2} + p^{2} T^{4} \) 2.89.a_afa
97$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 14 T + p T^{2} ) \) 2.97.e_cc
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

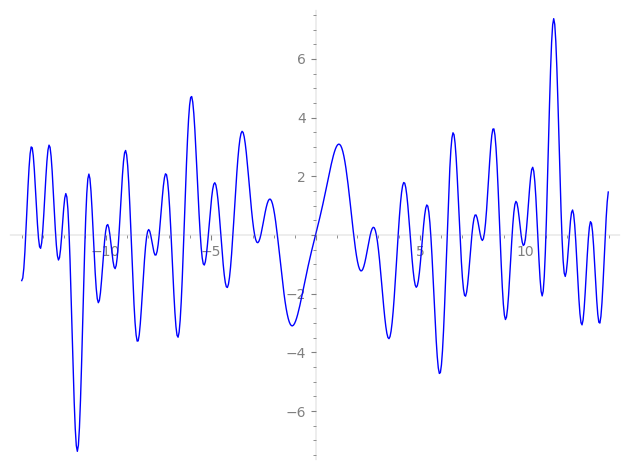
Imaginary part of the first few zeros on the critical line

−9.367877741844543050193015393776, −8.790645869348743541583890140431, −8.035717308600831141301879015920, −7.85432091676046990884579057078, −7.45083567807958670352178173490, −6.88378748099844220672693140137, −6.27231158206486611716078998519, −5.49196956912349091149082758541, −5.10878103773446000549867404225, −4.51086264680998032873079294263, −3.93773837536640582704719617912, −2.90061416096460280548678209478, −2.60708411241997444998295536301, −1.81960830191351705336228642595, 0, 1.81960830191351705336228642595, 2.60708411241997444998295536301, 2.90061416096460280548678209478, 3.93773837536640582704719617912, 4.51086264680998032873079294263, 5.10878103773446000549867404225, 5.49196956912349091149082758541, 6.27231158206486611716078998519, 6.88378748099844220672693140137, 7.45083567807958670352178173490, 7.85432091676046990884579057078, 8.035717308600831141301879015920, 8.790645869348743541583890140431, 9.367877741844543050193015393776

Graph of the $Z$-function along the critical line