↑

Properties

Label 4-777e2-1.1-c1e2-0-27
Degree $4$
Conductor $603729$
Sign $1$
Analytic cond. $38.4942$
Root an. cond. $2.49085$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2·2-s + 2·3-s − 4-s − 5-s + 4·6-s + 4·7-s − 8·8-s + 3·9-s − 2·10-s − 3·11-s − 2·12-s + 5·13-s + 8·14-s − 2·15-s − 7·16-s − 5·17-s + 6·18-s − 5·19-s + 20-s + 8·21-s − 6·22-s − 23-s − 16·24-s + 5·25-s + 10·26-s + 4·27-s − 4·28-s + ⋯
L(s)  = 1  + 1.41·2-s + 1.15·3-s − 1/2·4-s − 0.447·5-s + 1.63·6-s + 1.51·7-s − 2.82·8-s + 9-s − 0.632·10-s − 0.904·11-s − 0.577·12-s + 1.38·13-s + 2.13·14-s − 0.516·15-s − 7/4·16-s − 1.21·17-s + 1.41·18-s − 1.14·19-s + 0.223·20-s + 1.74·21-s − 1.27·22-s − 0.208·23-s − 3.26·24-s + 25-s + 1.96·26-s + 0.769·27-s − 0.755·28-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 603729 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 603729 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(603729\)    =    \(3^{2} \cdot 7^{2} \cdot 37^{2}\)
Sign: $1$
Analytic conductor: \(38.4942\)
Root analytic conductor: \(2.49085\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 603729,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(4.188893197\)
\(L(\frac12)\) \(\approx\) \(4.188893197\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad3$C_1$ \( ( 1 - T )^{2} \)
7$C_2$ \( 1 - 4 T + p T^{2} \)
37$C_2$ \( 1 + 10 T + p T^{2} \)
good2$C_2$ \( ( 1 - T + p T^{2} )^{2} \) 2.2.ac_f
5$C_2^2$ \( 1 + T - 4 T^{2} + p T^{3} + p^{2} T^{4} \) 2.5.b_ae
11$C_2^2$ \( 1 + 3 T - 2 T^{2} + 3 p T^{3} + p^{2} T^{4} \) 2.11.d_ac
13$C_2$ \( ( 1 - 7 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.13.af_m
17$C_2^2$ \( 1 + 5 T + 8 T^{2} + 5 p T^{3} + p^{2} T^{4} \) 2.17.f_i
19$C_2^2$ \( 1 + 5 T + 6 T^{2} + 5 p T^{3} + p^{2} T^{4} \) 2.19.f_g
23$C_2^2$ \( 1 + T - 22 T^{2} + p T^{3} + p^{2} T^{4} \) 2.23.b_aw
29$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.29.am_dq
31$C_2^2$ \( 1 + T - 30 T^{2} + p T^{3} + p^{2} T^{4} \) 2.31.b_abe
41$C_2^2$ \( 1 - 3 T - 32 T^{2} - 3 p T^{3} + p^{2} T^{4} \) 2.41.ad_abg
43$C_2$ \( ( 1 - 8 T + p T^{2} )^{2} \) 2.43.aq_fu
47$C_2^2$ \( 1 - 7 T + 2 T^{2} - 7 p T^{3} + p^{2} T^{4} \) 2.47.ah_c
53$C_2^2$ \( 1 + 9 T + 28 T^{2} + 9 p T^{3} + p^{2} T^{4} \) 2.53.j_bc
59$C_2^2$ \( 1 - 3 T - 50 T^{2} - 3 p T^{3} + p^{2} T^{4} \) 2.59.ad_aby
61$C_2^2$ \( 1 - 5 T - 36 T^{2} - 5 p T^{3} + p^{2} T^{4} \) 2.61.af_abk
67$C_2$ \( ( 1 + 12 T + p T^{2} )^{2} \) 2.67.y_ks
71$C_2^2$ \( 1 + 9 T + 10 T^{2} + 9 p T^{3} + p^{2} T^{4} \) 2.71.j_k
73$C_2^2$ \( 1 - 13 T + 96 T^{2} - 13 p T^{3} + p^{2} T^{4} \) 2.73.an_ds
79$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 17 T + p T^{2} ) \) 2.79.n_dm
83$C_2^2$ \( 1 - 9 T - 2 T^{2} - 9 p T^{3} + p^{2} T^{4} \) 2.83.aj_ac
89$C_2$ \( ( 1 - 10 T + p T^{2} )^{2} \) 2.89.au_ks
97$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.97.e_hq
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

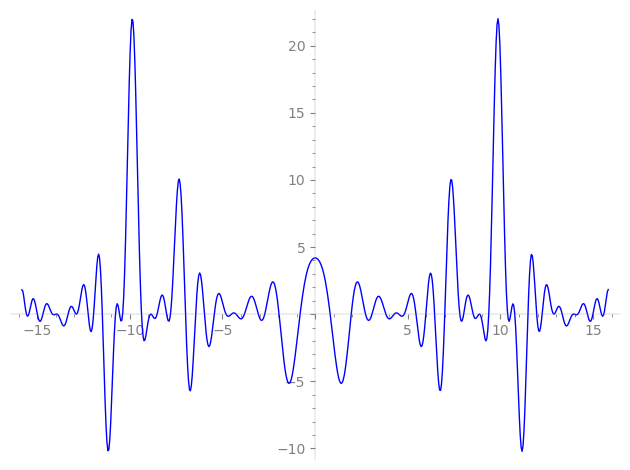
Imaginary part of the first few zeros on the critical line

−10.55500979043813526670898253007, −10.38732728117527163327020883850, −9.368771290722854374336838134550, −8.881957219685052861585491542107, −8.846365509422668895453570182584, −8.528468252029458003910140189441, −8.015476869895366321034404616676, −7.80672802735532261346130494553, −6.99410077569521569697328331149, −6.44828454895607037845660204968, −5.97218296959038909486232100345, −5.44215338823572610251411341403, −4.80790393443936163795753964326, −4.51619515618176634772654080992, −4.26606800691480002515751050307, −3.81730682928390817425038316375, −3.06706190333854369301596969185, −2.71982837509496168380711952592, −1.94771421880257108278350233886, −0.811248963153978711797153603620, 0.811248963153978711797153603620, 1.94771421880257108278350233886, 2.71982837509496168380711952592, 3.06706190333854369301596969185, 3.81730682928390817425038316375, 4.26606800691480002515751050307, 4.51619515618176634772654080992, 4.80790393443936163795753964326, 5.44215338823572610251411341403, 5.97218296959038909486232100345, 6.44828454895607037845660204968, 6.99410077569521569697328331149, 7.80672802735532261346130494553, 8.015476869895366321034404616676, 8.528468252029458003910140189441, 8.846365509422668895453570182584, 8.881957219685052861585491542107, 9.368771290722854374336838134550, 10.38732728117527163327020883850, 10.55500979043813526670898253007

Graph of the $Z$-function along the critical line