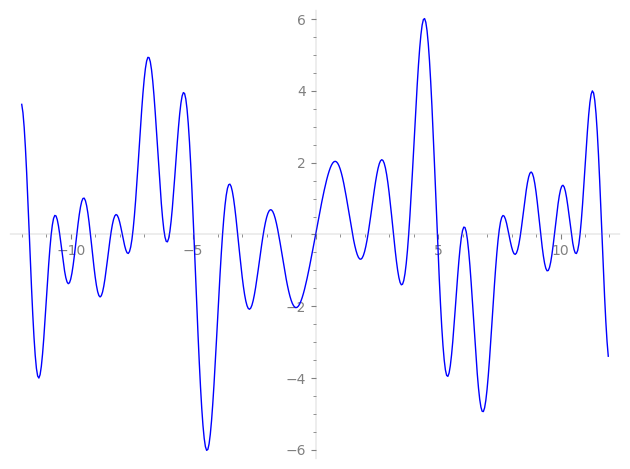
| L(s) = 1 | − 2-s + 3-s + 4-s + 5-s − 6-s − 8-s + 9-s − 10-s − 5·11-s + 12-s + 6·13-s + 15-s + 16-s + 2·17-s − 18-s + 19-s + 20-s + 5·22-s − 9·23-s − 24-s − 4·25-s − 6·26-s + 27-s − 8·29-s − 30-s + 4·31-s − 32-s + ⋯ |
| L(s) = 1 | − 0.707·2-s + 0.577·3-s + 1/2·4-s + 0.447·5-s − 0.408·6-s − 0.353·8-s + 1/3·9-s − 0.316·10-s − 1.50·11-s + 0.288·12-s + 1.66·13-s + 0.258·15-s + 1/4·16-s + 0.485·17-s − 0.235·18-s + 0.229·19-s + 0.223·20-s + 1.06·22-s − 1.87·23-s − 0.204·24-s − 4/5·25-s − 1.17·26-s + 0.192·27-s − 1.48·29-s − 0.182·30-s + 0.718·31-s − 0.176·32-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 5586 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 5586 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 + T \) | |
| 3 | \( 1 - T \) | |
| 7 | \( 1 \) | |
| 19 | \( 1 - T \) | |
| good | 5 | \( 1 - T + p T^{2} \) | 1.5.ab |
| 11 | \( 1 + 5 T + p T^{2} \) | 1.11.f |
| 13 | \( 1 - 6 T + p T^{2} \) | 1.13.ag |
| 17 | \( 1 - 2 T + p T^{2} \) | 1.17.ac |
| 23 | \( 1 + 9 T + p T^{2} \) | 1.23.j |
| 29 | \( 1 + 8 T + p T^{2} \) | 1.29.i |
| 31 | \( 1 - 4 T + p T^{2} \) | 1.31.ae |
| 37 | \( 1 + 4 T + p T^{2} \) | 1.37.e |
| 41 | \( 1 + 4 T + p T^{2} \) | 1.41.e |
| 43 | \( 1 - T + p T^{2} \) | 1.43.ab |
| 47 | \( 1 + T + p T^{2} \) | 1.47.b |
| 53 | \( 1 + 8 T + p T^{2} \) | 1.53.i |
| 59 | \( 1 + 6 T + p T^{2} \) | 1.59.g |
| 61 | \( 1 + 15 T + p T^{2} \) | 1.61.p |
| 67 | \( 1 + 10 T + p T^{2} \) | 1.67.k |
| 71 | \( 1 + 6 T + p T^{2} \) | 1.71.g |
| 73 | \( 1 - 9 T + p T^{2} \) | 1.73.aj |
| 79 | \( 1 - 12 T + p T^{2} \) | 1.79.am |
| 83 | \( 1 - 11 T + p T^{2} \) | 1.83.al |
| 89 | \( 1 - 2 T + p T^{2} \) | 1.89.ac |
| 97 | \( 1 + 8 T + p T^{2} \) | 1.97.i |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−7.893214339425903175864012821762, −7.47462993767186543952325946572, −6.16920664408130467210566040493, −5.96904321649093420221628889363, −4.97086522984237863596677543174, −3.80005450215509130217112965369, −3.18100712092445641569787101280, −2.13877068104695033726734903958, −1.50966308789600413052860012960, 0,
1.50966308789600413052860012960, 2.13877068104695033726734903958, 3.18100712092445641569787101280, 3.80005450215509130217112965369, 4.97086522984237863596677543174, 5.96904321649093420221628889363, 6.16920664408130467210566040493, 7.47462993767186543952325946572, 7.893214339425903175864012821762