| L(s) = 1 | − 2·3-s − 5-s − 4·7-s + 9-s + 6·13-s + 2·15-s + 8·21-s + 8·23-s + 25-s + 4·27-s − 29-s − 8·31-s + 4·35-s − 12·39-s + 6·41-s + 2·43-s − 45-s + 2·47-s + 9·49-s − 6·53-s − 12·59-s − 6·61-s − 4·63-s − 6·65-s − 16·67-s − 16·69-s + 4·73-s + ⋯ |
| L(s) = 1 | − 1.15·3-s − 0.447·5-s − 1.51·7-s + 1/3·9-s + 1.66·13-s + 0.516·15-s + 1.74·21-s + 1.66·23-s + 1/5·25-s + 0.769·27-s − 0.185·29-s − 1.43·31-s + 0.676·35-s − 1.92·39-s + 0.937·41-s + 0.304·43-s − 0.149·45-s + 0.291·47-s + 9/7·49-s − 0.824·53-s − 1.56·59-s − 0.768·61-s − 0.503·63-s − 0.744·65-s − 1.95·67-s − 1.92·69-s + 0.468·73-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 2320 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2320 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 \) | |
| 5 | \( 1 + T \) | |
| 29 | \( 1 + T \) | |
| good | 3 | \( 1 + 2 T + p T^{2} \) | 1.3.c |
| 7 | \( 1 + 4 T + p T^{2} \) | 1.7.e |
| 11 | \( 1 + p T^{2} \) | 1.11.a |
| 13 | \( 1 - 6 T + p T^{2} \) | 1.13.ag |
| 17 | \( 1 + p T^{2} \) | 1.17.a |
| 19 | \( 1 + p T^{2} \) | 1.19.a |
| 23 | \( 1 - 8 T + p T^{2} \) | 1.23.ai |
| 31 | \( 1 + 8 T + p T^{2} \) | 1.31.i |
| 37 | \( 1 + p T^{2} \) | 1.37.a |
| 41 | \( 1 - 6 T + p T^{2} \) | 1.41.ag |
| 43 | \( 1 - 2 T + p T^{2} \) | 1.43.ac |
| 47 | \( 1 - 2 T + p T^{2} \) | 1.47.ac |
| 53 | \( 1 + 6 T + p T^{2} \) | 1.53.g |
| 59 | \( 1 + 12 T + p T^{2} \) | 1.59.m |
| 61 | \( 1 + 6 T + p T^{2} \) | 1.61.g |
| 67 | \( 1 + 16 T + p T^{2} \) | 1.67.q |
| 71 | \( 1 + p T^{2} \) | 1.71.a |
| 73 | \( 1 - 4 T + p T^{2} \) | 1.73.ae |
| 79 | \( 1 - 8 T + p T^{2} \) | 1.79.ai |
| 83 | \( 1 + 8 T + p T^{2} \) | 1.83.i |
| 89 | \( 1 + 10 T + p T^{2} \) | 1.89.k |
| 97 | \( 1 - 8 T + p T^{2} \) | 1.97.ai |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
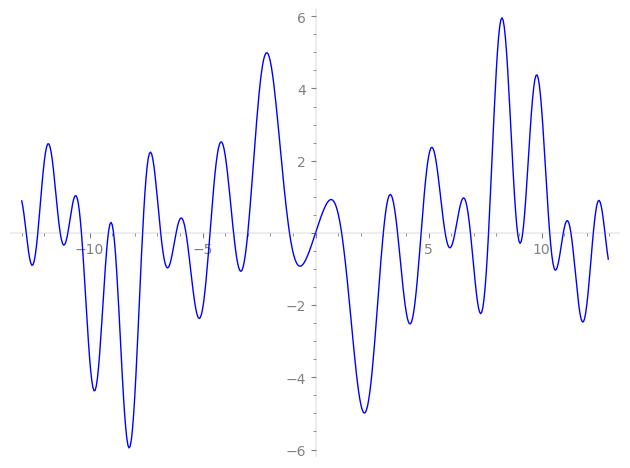
Imaginary part of the first few zeros on the critical line
−8.937132373963094918098131062866, −7.65300759320240801334039199640, −6.85193771012451657253517149866, −6.16896013879507699937469003155, −5.73359443936300595868147392633, −4.67040862570166046478650993910, −3.62782408323068056564266888657, −2.99746001243481172043393830968, −1.15339555479317514330126356504, 0,
1.15339555479317514330126356504, 2.99746001243481172043393830968, 3.62782408323068056564266888657, 4.67040862570166046478650993910, 5.73359443936300595868147392633, 6.16896013879507699937469003155, 6.85193771012451657253517149866, 7.65300759320240801334039199640, 8.937132373963094918098131062866