↑

Properties

Label 4-1568e2-1.1-c1e2-0-10
Degree $4$
Conductor $2458624$
Sign $1$
Analytic cond. $156.763$
Root an. cond. $3.53843$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2·3-s + 3·9-s + 4·11-s − 8·13-s + 2·17-s + 6·19-s − 8·23-s + 5·25-s + 10·27-s + 4·29-s + 4·31-s + 8·33-s − 10·37-s − 16·39-s − 20·41-s + 8·43-s − 4·47-s + 4·51-s + 2·53-s + 12·57-s − 10·59-s + 8·61-s + 8·67-s − 16·69-s + 6·73-s + 10·75-s + 16·79-s + ⋯
L(s)  = 1  + 1.15·3-s + 9-s + 1.20·11-s − 2.21·13-s + 0.485·17-s + 1.37·19-s − 1.66·23-s + 25-s + 1.92·27-s + 0.742·29-s + 0.718·31-s + 1.39·33-s − 1.64·37-s − 2.56·39-s − 3.12·41-s + 1.21·43-s − 0.583·47-s + 0.560·51-s + 0.274·53-s + 1.58·57-s − 1.30·59-s + 1.02·61-s + 0.977·67-s − 1.92·69-s + 0.702·73-s + 1.15·75-s + 1.80·79-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2458624 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2458624 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(2458624\)    =    \(2^{10} \cdot 7^{4}\)
Sign: $1$
Analytic conductor: \(156.763\)
Root analytic conductor: \(3.53843\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 2458624,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(3.618417482\)
\(L(\frac12)\) \(\approx\) \(3.618417482\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
7 \( 1 \)
good3$C_2^2$ \( 1 - 2 T + T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.3.ac_b
5$C_2^2$ \( 1 - p T^{2} + p^{2} T^{4} \) 2.5.a_af
11$C_2^2$ \( 1 - 4 T + 5 T^{2} - 4 p T^{3} + p^{2} T^{4} \) 2.11.ae_f
13$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.13.i_bq
17$C_2^2$ \( 1 - 2 T - 13 T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.17.ac_an
19$C_2^2$ \( 1 - 6 T + 17 T^{2} - 6 p T^{3} + p^{2} T^{4} \) 2.19.ag_r
23$C_2^2$ \( 1 + 8 T + 41 T^{2} + 8 p T^{3} + p^{2} T^{4} \) 2.23.i_bp
29$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.29.ae_ck
31$C_2$ \( ( 1 - 11 T + p T^{2} )( 1 + 7 T + p T^{2} ) \) 2.31.ae_ap
37$C_2$ \( ( 1 - T + p T^{2} )( 1 + 11 T + p T^{2} ) \) 2.37.k_cl
41$C_2$ \( ( 1 + 10 T + p T^{2} )^{2} \) 2.41.u_ha
43$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.43.ai_dy
47$C_2^2$ \( 1 + 4 T - 31 T^{2} + 4 p T^{3} + p^{2} T^{4} \) 2.47.e_abf
53$C_2^2$ \( 1 - 2 T - 49 T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.53.ac_abx
59$C_2^2$ \( 1 + 10 T + 41 T^{2} + 10 p T^{3} + p^{2} T^{4} \) 2.59.k_bp
61$C_2^2$ \( 1 - 8 T + 3 T^{2} - 8 p T^{3} + p^{2} T^{4} \) 2.61.ai_d
67$C_2^2$ \( 1 - 8 T - 3 T^{2} - 8 p T^{3} + p^{2} T^{4} \) 2.67.ai_ad
71$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.71.a_fm
73$C_2^2$ \( 1 - 6 T - 37 T^{2} - 6 p T^{3} + p^{2} T^{4} \) 2.73.ag_abl
79$C_2^2$ \( 1 - 16 T + 177 T^{2} - 16 p T^{3} + p^{2} T^{4} \) 2.79.aq_gv
83$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.83.ae_go
89$C_2^2$ \( 1 + 18 T + 235 T^{2} + 18 p T^{3} + p^{2} T^{4} \) 2.89.s_jb
97$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.97.e_hq
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

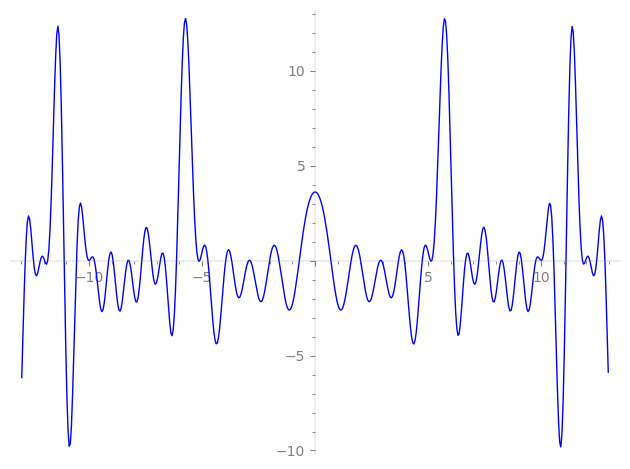
Imaginary part of the first few zeros on the critical line

−9.764664668741302425296577013520, −9.131990479126547086206410105317, −8.935618744639606178158548065259, −8.288160011650115988026063046662, −8.226742755290609853996172103233, −7.66673133820314280638966525338, −7.24502425935227376474024920526, −6.84796716705882411980144600197, −6.65495064580876221518634699169, −6.13014693493831836706981825908, −5.16370727224857433240921688883, −5.10182222428006508201329252193, −4.74148336838648099636782402493, −3.95419917458395826946989809104, −3.69065127170005976181181153096, −2.93991732126155711150269897491, −2.86626175830223330806690385101, −2.01399891433192791332222017452, −1.59508245037601386228854357373, −0.69972999514909345743633137145, 0.69972999514909345743633137145, 1.59508245037601386228854357373, 2.01399891433192791332222017452, 2.86626175830223330806690385101, 2.93991732126155711150269897491, 3.69065127170005976181181153096, 3.95419917458395826946989809104, 4.74148336838648099636782402493, 5.10182222428006508201329252193, 5.16370727224857433240921688883, 6.13014693493831836706981825908, 6.65495064580876221518634699169, 6.84796716705882411980144600197, 7.24502425935227376474024920526, 7.66673133820314280638966525338, 8.226742755290609853996172103233, 8.288160011650115988026063046662, 8.935618744639606178158548065259, 9.131990479126547086206410105317, 9.764664668741302425296577013520

Graph of the $Z$-function along the critical line