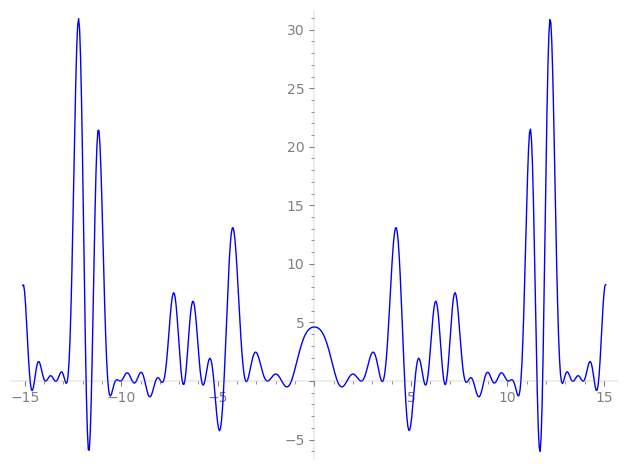
| L(s) = 1 | − 2-s + 3·3-s + 6·5-s − 3·6-s + 8-s + 6·9-s − 6·10-s − 6·11-s + 5·13-s + 18·15-s − 16-s + 3·17-s − 6·18-s + 5·19-s + 6·22-s − 6·23-s + 3·24-s + 17·25-s − 5·26-s + 9·27-s + 3·29-s − 18·30-s − 4·31-s − 18·33-s − 3·34-s + 7·37-s − 5·38-s + ⋯ |
| L(s) = 1 | − 0.707·2-s + 1.73·3-s + 2.68·5-s − 1.22·6-s + 0.353·8-s + 2·9-s − 1.89·10-s − 1.80·11-s + 1.38·13-s + 4.64·15-s − 1/4·16-s + 0.727·17-s − 1.41·18-s + 1.14·19-s + 1.27·22-s − 1.25·23-s + 0.612·24-s + 17/5·25-s − 0.980·26-s + 1.73·27-s + 0.557·29-s − 3.28·30-s − 0.718·31-s − 3.13·33-s − 0.514·34-s + 1.15·37-s − 0.811·38-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 777924 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 777924 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(4.613492971\) |
| \(L(\frac12)\) |
\(\approx\) |
\(4.613492971\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( 1 + T + T^{2} \) |
| 3 | $C_2$ | \( 1 - p T + p T^{2} \) |
| 7 | | \( 1 \) |
| good | 5 | $C_2$ | \( ( 1 - 3 T + p T^{2} )^{2} \) |
| 11 | $C_2$ | \( ( 1 + 3 T + p T^{2} )^{2} \) |
| 13 | $C_2$ | \( ( 1 - 7 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) |
| 17 | $C_2^2$ | \( 1 - 3 T - 8 T^{2} - 3 p T^{3} + p^{2} T^{4} \) |
| 19 | $C_2^2$ | \( 1 - 5 T + 6 T^{2} - 5 p T^{3} + p^{2} T^{4} \) |
| 23 | $C_2$ | \( ( 1 + 3 T + p T^{2} )^{2} \) |
| 29 | $C_2^2$ | \( 1 - 3 T - 20 T^{2} - 3 p T^{3} + p^{2} T^{4} \) |
| 31 | $C_2$ | \( ( 1 - 7 T + p T^{2} )( 1 + 11 T + p T^{2} ) \) |
| 37 | $C_2^2$ | \( 1 - 7 T + 12 T^{2} - 7 p T^{3} + p^{2} T^{4} \) |
| 41 | $C_2^2$ | \( 1 + 9 T + 40 T^{2} + 9 p T^{3} + p^{2} T^{4} \) |
| 43 | $C_2^2$ | \( 1 + 11 T + 78 T^{2} + 11 p T^{3} + p^{2} T^{4} \) |
| 47 | $C_2^2$ | \( 1 - p T^{2} + p^{2} T^{4} \) |
| 53 | $C_2^2$ | \( 1 - 3 T - 44 T^{2} - 3 p T^{3} + p^{2} T^{4} \) |
| 59 | $C_2^2$ | \( 1 - 12 T + 85 T^{2} - 12 p T^{3} + p^{2} T^{4} \) |
| 61 | $C_2^2$ | \( 1 - 2 T - 57 T^{2} - 2 p T^{3} + p^{2} T^{4} \) |
| 67 | $C_2^2$ | \( 1 - 4 T - 51 T^{2} - 4 p T^{3} + p^{2} T^{4} \) |
| 71 | $C_2$ | \( ( 1 + p T^{2} )^{2} \) |
| 73 | $C_2^2$ | \( 1 - 11 T + 48 T^{2} - 11 p T^{3} + p^{2} T^{4} \) |
| 79 | $C_2^2$ | \( 1 + 8 T - 15 T^{2} + 8 p T^{3} + p^{2} T^{4} \) |
| 83 | $C_2^2$ | \( 1 - 3 T - 74 T^{2} - 3 p T^{3} + p^{2} T^{4} \) |
| 89 | $C_2^2$ | \( 1 - 15 T + 136 T^{2} - 15 p T^{3} + p^{2} T^{4} \) |
| 97 | $C_2^2$ | \( 1 + T - 96 T^{2} + p T^{3} + p^{2} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−10.07072108260706918765824461688, −10.03263677906980414856681519564, −9.430145099193544995087610682419, −9.218546075326502654405362567215, −8.782038014004441646293455588751, −8.223166459504496700769015838932, −7.954341358824569538010073302881, −7.81096689234352333833119569384, −6.84223915049579025002789939707, −6.70975832202898668359737135878, −5.84165783738821365989698170307, −5.67047449022463314232935578372, −5.20588798342296759170232647765, −4.67909086051270661942279205293, −3.55813429650824455781993447186, −3.48027797800182904908882687631, −2.44921689129977520474181430241, −2.40164852297358847021678028369, −1.69013744921169547794207668462, −1.19074667564211791699421356238,
1.19074667564211791699421356238, 1.69013744921169547794207668462, 2.40164852297358847021678028369, 2.44921689129977520474181430241, 3.48027797800182904908882687631, 3.55813429650824455781993447186, 4.67909086051270661942279205293, 5.20588798342296759170232647765, 5.67047449022463314232935578372, 5.84165783738821365989698170307, 6.70975832202898668359737135878, 6.84223915049579025002789939707, 7.81096689234352333833119569384, 7.954341358824569538010073302881, 8.223166459504496700769015838932, 8.782038014004441646293455588751, 9.218546075326502654405362567215, 9.430145099193544995087610682419, 10.03263677906980414856681519564, 10.07072108260706918765824461688
