↑

Properties

Label 4-864e2-1.1-c1e2-0-26
Degree $4$
Conductor $746496$
Sign $1$
Analytic cond. $47.5972$
Root an. cond. $2.62660$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

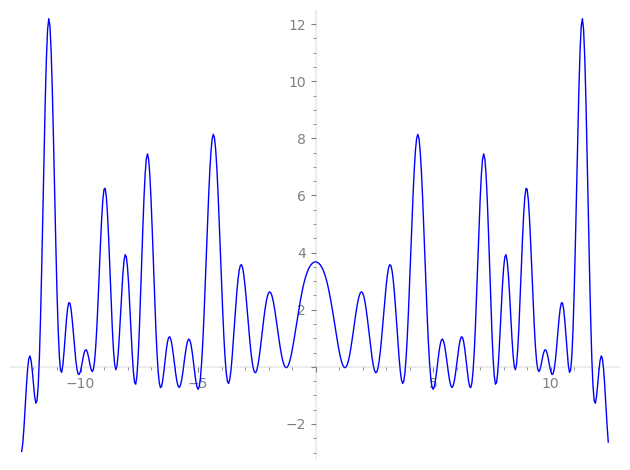
L(s)  = 1  + 4·5-s + 2·13-s + 12·17-s + 2·25-s + 16·29-s − 10·37-s + 16·41-s − 13·49-s + 8·53-s + 6·61-s + 8·65-s + 18·73-s + 48·85-s − 4·89-s + 2·97-s − 20·109-s − 20·113-s − 18·121-s − 28·125-s + 127-s + 131-s + 137-s + 139-s + 64·145-s + 149-s + 151-s + 157-s + ⋯
L(s)  = 1  + 1.78·5-s + 0.554·13-s + 2.91·17-s + 2/5·25-s + 2.97·29-s − 1.64·37-s + 2.49·41-s − 1.85·49-s + 1.09·53-s + 0.768·61-s + 0.992·65-s + 2.10·73-s + 5.20·85-s − 0.423·89-s + 0.203·97-s − 1.91·109-s − 1.88·113-s − 1.63·121-s − 2.50·125-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 5.31·145-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 746496 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 746496 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(746496\)    =    \(2^{10} \cdot 3^{6}\)
Sign: $1$
Analytic conductor: \(47.5972\)
Root analytic conductor: \(2.62660\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 746496,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(3.674012128\)
\(L(\frac12)\) \(\approx\) \(3.674012128\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
3 \( 1 \)
good5$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.5.ae_o
7$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.7.a_n
11$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.11.a_s
13$C_2$ \( ( 1 - T + p T^{2} )^{2} \) 2.13.ac_bb
17$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.17.am_cs
19$C_2$ \( ( 1 - 5 T + p T^{2} )( 1 + 5 T + p T^{2} ) \) 2.19.a_n
23$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.23.a_k
29$C_2$ \( ( 1 - 8 T + p T^{2} )^{2} \) 2.29.aq_es
31$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.31.a_ac
37$C_2$ \( ( 1 + 5 T + p T^{2} )^{2} \) 2.37.k_dv
41$C_2$ \( ( 1 - 8 T + p T^{2} )^{2} \) 2.41.aq_fq
43$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.43.a_cs
47$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.47.a_ag
53$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.53.ai_es
59$C_2$ \( ( 1 - 14 T + p T^{2} )( 1 + 14 T + p T^{2} ) \) 2.59.a_ada
61$C_2$ \( ( 1 - 3 T + p T^{2} )^{2} \) 2.61.ag_fb
67$C_2$ \( ( 1 - 13 T + p T^{2} )( 1 + 13 T + p T^{2} ) \) 2.67.a_abj
71$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.71.a_ew
73$C_2$ \( ( 1 - 9 T + p T^{2} )^{2} \) 2.73.as_it
79$C_2$ \( ( 1 - 11 T + p T^{2} )( 1 + 11 T + p T^{2} ) \) 2.79.a_bl
83$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.83.a_w
89$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.89.e_ha
97$C_2$ \( ( 1 - T + p T^{2} )^{2} \) 2.97.ac_hn
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.452903426046461019559543114245, −7.76557077946649787116094304644, −7.57195972780640499908950962067, −6.71110929993388671275045148454, −6.43257826526562631052914578190, −5.98787564282874923662914045287, −5.61589452328752483822361023345, −5.17169676997140923385106697279, −4.85942281184589681377721538834, −3.82323482337136190917747918800, −3.58529057716851715664298339034, −2.66421157652505017015711163951, −2.46655581258054430403163598781, −1.29992084912787334744679961781, −1.19497678164755144713673653335, 1.19497678164755144713673653335, 1.29992084912787334744679961781, 2.46655581258054430403163598781, 2.66421157652505017015711163951, 3.58529057716851715664298339034, 3.82323482337136190917747918800, 4.85942281184589681377721538834, 5.17169676997140923385106697279, 5.61589452328752483822361023345, 5.98787564282874923662914045287, 6.43257826526562631052914578190, 6.71110929993388671275045148454, 7.57195972780640499908950962067, 7.76557077946649787116094304644, 8.452903426046461019559543114245

Graph of the $Z$-function along the critical line