↑

Properties

Label 4-623808-1.1-c1e2-0-18
Degree $4$
Conductor $623808$
Sign $1$
Analytic cond. $39.7745$
Root an. cond. $2.51131$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $0$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2·2-s − 3-s + 2·4-s − 2·6-s − 2·7-s + 9-s − 2·12-s − 4·14-s − 4·16-s + 2·18-s + 4·19-s + 2·21-s + 3·25-s − 27-s − 4·28-s + 6·29-s − 8·32-s + 2·36-s + 8·38-s + 12·41-s + 4·42-s + 4·48-s − 7·49-s + 6·50-s − 16·53-s − 2·54-s − 4·57-s + ⋯
L(s)  = 1  + 1.41·2-s − 0.577·3-s + 4-s − 0.816·6-s − 0.755·7-s + 1/3·9-s − 0.577·12-s − 1.06·14-s − 16-s + 0.471·18-s + 0.917·19-s + 0.436·21-s + 3/5·25-s − 0.192·27-s − 0.755·28-s + 1.11·29-s − 1.41·32-s + 1/3·36-s + 1.29·38-s + 1.87·41-s + 0.617·42-s + 0.577·48-s − 49-s + 0.848·50-s − 2.19·53-s − 0.272·54-s − 0.529·57-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 623808 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 623808 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(623808\)    =    \(2^{6} \cdot 3^{3} \cdot 19^{2}\)
Sign: $1$
Analytic conductor: \(39.7745\)
Root analytic conductor: \(2.51131\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 623808,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(2.725542240\)
\(L(\frac12)\) \(\approx\) \(2.725542240\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_2$ \( 1 - p T + p T^{2} \)
3$C_1$ \( 1 + T \)
19$C_2$ \( 1 - 4 T + p T^{2} \)
good5$C_2^2$ \( 1 - 3 T^{2} + p^{2} T^{4} \) 2.5.a_ad
7$C_2$$\times$$C_2$ \( ( 1 - T + p T^{2} )( 1 + 3 T + p T^{2} ) \) 2.7.c_l
11$C_2^2$ \( 1 + 5 T^{2} + p^{2} T^{4} \) 2.11.a_f
13$C_2^2$ \( 1 + 14 T^{2} + p^{2} T^{4} \) 2.13.a_o
17$C_2^2$ \( 1 - T^{2} + p^{2} T^{4} \) 2.17.a_ab
23$C_2^2$ \( 1 + 22 T^{2} + p^{2} T^{4} \) 2.23.a_w
29$C_2$$\times$$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + p T^{2} ) \) 2.29.ag_cg
31$C_2^2$ \( 1 + 50 T^{2} + p^{2} T^{4} \) 2.31.a_by
37$C_2^2$ \( 1 - 10 T^{2} + p^{2} T^{4} \) 2.37.a_ak
41$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.41.am_dy
43$C_2$ \( ( 1 - T + p T^{2} )( 1 + T + p T^{2} ) \) 2.43.a_dh
47$C_2^2$ \( 1 - 41 T^{2} + p^{2} T^{4} \) 2.47.a_abp
53$C_2$$\times$$C_2$ \( ( 1 + 4 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.53.q_fy
59$C_2$$\times$$C_2$ \( ( 1 + 2 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.59.o_fm
61$C_2$ \( ( 1 - 7 T + p T^{2} )( 1 + 7 T + p T^{2} ) \) 2.61.a_cv
67$C_2^2$ \( 1 + 114 T^{2} + p^{2} T^{4} \) 2.67.a_ek
71$C_2$$\times$$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 - 6 T + p T^{2} ) \) 2.71.as_ig
73$C_2$$\times$$C_2$ \( ( 1 - 7 T + p T^{2} )( 1 + 5 T + p T^{2} ) \) 2.73.ac_eh
79$C_2^2$ \( 1 - 82 T^{2} + p^{2} T^{4} \) 2.79.a_ade
83$C_2^2$ \( 1 - 86 T^{2} + p^{2} T^{4} \) 2.83.a_adi
89$C_2$$\times$$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.89.ae_fq
97$C_2^2$ \( 1 - 94 T^{2} + p^{2} T^{4} \) 2.97.a_adq
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

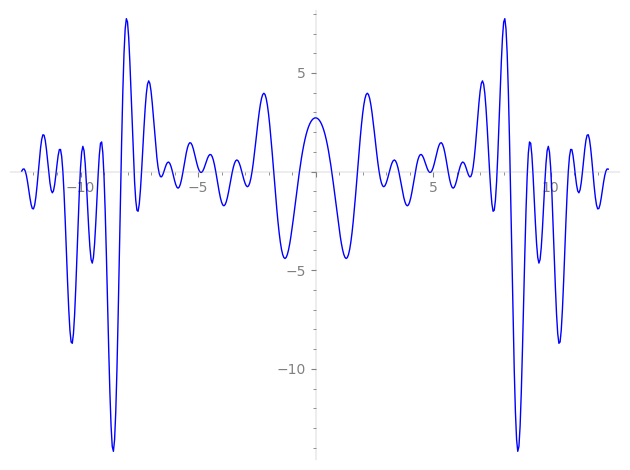
Imaginary part of the first few zeros on the critical line

−8.277428130720311882410021609053, −7.72074019123892367060058219860, −7.40252425866461248577478481593, −6.66975269698908495708139711285, −6.45210028139883725944800467893, −6.09046766708034068285154203500, −5.63925540470909806777829255198, −4.92808060694292525213902864506, −4.81403449653729736363829507663, −4.24668130207193891813902026749, −3.54008919605456352382344280653, −3.13998640588981906978207603314, −2.70203224365569508635180457474, −1.78164709440621181415033988656, −0.68723497118330371982244874581, 0.68723497118330371982244874581, 1.78164709440621181415033988656, 2.70203224365569508635180457474, 3.13998640588981906978207603314, 3.54008919605456352382344280653, 4.24668130207193891813902026749, 4.81403449653729736363829507663, 4.92808060694292525213902864506, 5.63925540470909806777829255198, 6.09046766708034068285154203500, 6.45210028139883725944800467893, 6.66975269698908495708139711285, 7.40252425866461248577478481593, 7.72074019123892367060058219860, 8.277428130720311882410021609053

Graph of the $Z$-function along the critical line