↑

Properties

Label 4-1548800-1.1-c1e2-0-2
Degree $4$
Conductor $1548800$
Sign $1$
Analytic cond. $98.7528$
Root an. cond. $3.15237$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $0$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 3·5-s + 9-s + 4·13-s + 4·17-s + 4·25-s − 12·37-s + 16·41-s + 3·45-s − 2·49-s + 8·53-s + 8·61-s + 12·65-s + 12·73-s − 8·81-s + 12·85-s + 6·89-s + 8·97-s + 4·101-s − 12·109-s + 4·117-s + 121-s − 3·125-s + 127-s + 131-s + 137-s + 139-s + 149-s + ⋯
L(s)  = 1  + 1.34·5-s + 1/3·9-s + 1.10·13-s + 0.970·17-s + 4/5·25-s − 1.97·37-s + 2.49·41-s + 0.447·45-s − 2/7·49-s + 1.09·53-s + 1.02·61-s + 1.48·65-s + 1.40·73-s − 8/9·81-s + 1.30·85-s + 0.635·89-s + 0.812·97-s + 0.398·101-s − 1.14·109-s + 0.369·117-s + 1/11·121-s − 0.268·125-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1548800 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1548800 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(1548800\)    =    \(2^{9} \cdot 5^{2} \cdot 11^{2}\)
Sign: $1$
Analytic conductor: \(98.7528\)
Root analytic conductor: \(3.15237\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 1548800,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(3.582634456\)
\(L(\frac12)\) \(\approx\) \(3.582634456\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
5$C_2$ \( 1 - 3 T + p T^{2} \)
11$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
good3$C_2^2$ \( 1 - T^{2} + p^{2} T^{4} \) 2.3.a_ab
7$C_2^2$ \( 1 + 2 T^{2} + p^{2} T^{4} \) 2.7.a_c
13$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.13.ae_be
17$C_2$$\times$$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + p T^{2} ) \) 2.17.ae_bi
19$C_2^2$ \( 1 - 6 T^{2} + p^{2} T^{4} \) 2.19.a_ag
23$C_2^2$ \( 1 + 27 T^{2} + p^{2} T^{4} \) 2.23.a_bb
29$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.29.a_cg
31$C_2$ \( ( 1 - 9 T + p T^{2} )( 1 + 9 T + p T^{2} ) \) 2.31.a_at
37$C_2$$\times$$C_2$ \( ( 1 + 3 T + p T^{2} )( 1 + 9 T + p T^{2} ) \) 2.37.m_dx
41$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 - 6 T + p T^{2} ) \) 2.41.aq_fm
43$C_2^2$ \( 1 + 30 T^{2} + p^{2} T^{4} \) 2.43.a_be
47$C_2^2$ \( 1 - 30 T^{2} + p^{2} T^{4} \) 2.47.a_abe
53$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.53.ai_di
59$C_2^2$ \( 1 - 39 T^{2} + p^{2} T^{4} \) 2.59.a_abn
61$C_2$$\times$$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + p T^{2} ) \) 2.61.ai_es
67$C_2^2$ \( 1 + 119 T^{2} + p^{2} T^{4} \) 2.67.a_ep
71$C_2^2$ \( 1 - 43 T^{2} + p^{2} T^{4} \) 2.71.a_abr
73$C_2$$\times$$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.73.am_gk
79$C_2$ \( ( 1 - 14 T + p T^{2} )( 1 + 14 T + p T^{2} ) \) 2.79.a_abm
83$C_2^2$ \( 1 + 126 T^{2} + p^{2} T^{4} \) 2.83.a_ew
89$C_2$$\times$$C_2$ \( ( 1 - 15 T + p T^{2} )( 1 + 9 T + p T^{2} ) \) 2.89.ag_br
97$C_2$$\times$$C_2$ \( ( 1 - 7 T + p T^{2} )( 1 - T + p T^{2} ) \) 2.97.ai_ht
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

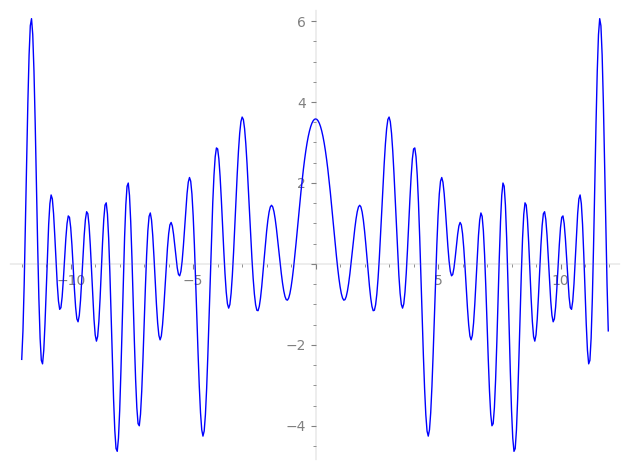
Imaginary part of the first few zeros on the critical line

−7.83290372054141537481868228159, −7.49234572226566462494801206786, −6.91510463035667026824565708484, −6.58534122582832805744775658662, −6.09281676983507833178986300809, −5.67028125142495685849123646544, −5.46179419306824427416170236178, −4.92143830910894627454482145619, −4.28491315989963807497385442400, −3.72182876109990058936915478178, −3.37409523502182206276709906233, −2.58747876159800445047620984190, −2.11882239301548230262866613091, −1.44443560708728800663264729853, −0.883553223544632301582395376375, 0.883553223544632301582395376375, 1.44443560708728800663264729853, 2.11882239301548230262866613091, 2.58747876159800445047620984190, 3.37409523502182206276709906233, 3.72182876109990058936915478178, 4.28491315989963807497385442400, 4.92143830910894627454482145619, 5.46179419306824427416170236178, 5.67028125142495685849123646544, 6.09281676983507833178986300809, 6.58534122582832805744775658662, 6.91510463035667026824565708484, 7.49234572226566462494801206786, 7.83290372054141537481868228159

Graph of the $Z$-function along the critical line