| L(s) = 1 | − 2-s − 3-s + 4-s + 6-s − 8-s + 9-s − 11-s − 12-s + 13-s + 16-s − 3·17-s − 18-s − 19-s + 22-s + 23-s + 24-s − 26-s − 27-s + 5·29-s + 6·31-s − 32-s + 33-s + 3·34-s + 36-s + 37-s + 38-s − 39-s + ⋯ |
| L(s) = 1 | − 0.707·2-s − 0.577·3-s + 1/2·4-s + 0.408·6-s − 0.353·8-s + 1/3·9-s − 0.301·11-s − 0.288·12-s + 0.277·13-s + 1/4·16-s − 0.727·17-s − 0.235·18-s − 0.229·19-s + 0.213·22-s + 0.208·23-s + 0.204·24-s − 0.196·26-s − 0.192·27-s + 0.928·29-s + 1.07·31-s − 0.176·32-s + 0.174·33-s + 0.514·34-s + 1/6·36-s + 0.164·37-s + 0.162·38-s − 0.160·39-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 95550 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 95550 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 + T \) | |
| 3 | \( 1 + T \) | |
| 5 | \( 1 \) | |
| 7 | \( 1 \) | |
| 13 | \( 1 - T \) | |
| good | 11 | \( 1 + T + p T^{2} \) | 1.11.b |
| 17 | \( 1 + 3 T + p T^{2} \) | 1.17.d |
| 19 | \( 1 + T + p T^{2} \) | 1.19.b |
| 23 | \( 1 - T + p T^{2} \) | 1.23.ab |
| 29 | \( 1 - 5 T + p T^{2} \) | 1.29.af |
| 31 | \( 1 - 6 T + p T^{2} \) | 1.31.ag |
| 37 | \( 1 - T + p T^{2} \) | 1.37.ab |
| 41 | \( 1 + p T^{2} \) | 1.41.a |
| 43 | \( 1 + 3 T + p T^{2} \) | 1.43.d |
| 47 | \( 1 - 4 T + p T^{2} \) | 1.47.ae |
| 53 | \( 1 - 6 T + p T^{2} \) | 1.53.ag |
| 59 | \( 1 - 2 T + p T^{2} \) | 1.59.ac |
| 61 | \( 1 + T + p T^{2} \) | 1.61.b |
| 67 | \( 1 + 16 T + p T^{2} \) | 1.67.q |
| 71 | \( 1 - 6 T + p T^{2} \) | 1.71.ag |
| 73 | \( 1 - 5 T + p T^{2} \) | 1.73.af |
| 79 | \( 1 - 12 T + p T^{2} \) | 1.79.am |
| 83 | \( 1 + 6 T + p T^{2} \) | 1.83.g |
| 89 | \( 1 + p T^{2} \) | 1.89.a |
| 97 | \( 1 - 18 T + p T^{2} \) | 1.97.as |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
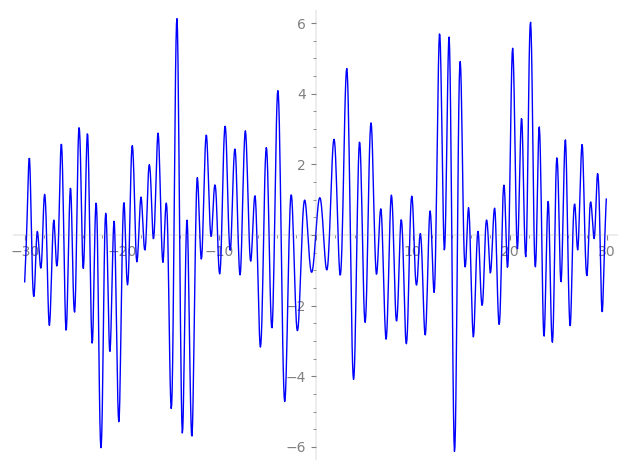
Imaginary part of the first few zeros on the critical line
−14.02506330444746, −13.35751396965511, −13.18665870583590, −12.39067938621057, −11.94907854721279, −11.64710327742717, −10.83746561583405, −10.73671483941863, −10.11584893537224, −9.703010842008325, −8.947158133409150, −8.696736211674818, −8.006644702219873, −7.612177995363603, −6.872317040510163, −6.512695081352070, −6.065231237007947, −5.367954823993558, −4.811081331952692, −4.252284870581360, −3.568101738772242, −2.734983436124995, −2.303861848963267, −1.416292007408473, −0.8076542459699346, 0,
0.8076542459699346, 1.416292007408473, 2.303861848963267, 2.734983436124995, 3.568101738772242, 4.252284870581360, 4.811081331952692, 5.367954823993558, 6.065231237007947, 6.512695081352070, 6.872317040510163, 7.612177995363603, 8.006644702219873, 8.696736211674818, 8.947158133409150, 9.703010842008325, 10.11584893537224, 10.73671483941863, 10.83746561583405, 11.64710327742717, 11.94907854721279, 12.39067938621057, 13.18665870583590, 13.35751396965511, 14.02506330444746