↑

Properties

Label 4-1425e2-1.1-c1e2-0-9
Degree $4$
Conductor $2030625$
Sign $1$
Analytic cond. $129.474$
Root an. cond. $3.37323$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $2$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2-s − 2·3-s − 2·4-s − 2·6-s − 3·8-s + 3·9-s − 8·11-s + 4·12-s + 4·13-s + 16-s − 2·17-s + 3·18-s − 2·19-s − 8·22-s + 2·23-s + 6·24-s + 4·26-s − 4·27-s + 6·29-s − 12·31-s + 2·32-s + 16·33-s − 2·34-s − 6·36-s + 10·37-s − 2·38-s − 8·39-s + ⋯
L(s)  = 1  + 0.707·2-s − 1.15·3-s − 4-s − 0.816·6-s − 1.06·8-s + 9-s − 2.41·11-s + 1.15·12-s + 1.10·13-s + 1/4·16-s − 0.485·17-s + 0.707·18-s − 0.458·19-s − 1.70·22-s + 0.417·23-s + 1.22·24-s + 0.784·26-s − 0.769·27-s + 1.11·29-s − 2.15·31-s + 0.353·32-s + 2.78·33-s − 0.342·34-s − 36-s + 1.64·37-s − 0.324·38-s − 1.28·39-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2030625 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2030625 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(2030625\)    =    \(3^{2} \cdot 5^{4} \cdot 19^{2}\)
Sign: $1$
Analytic conductor: \(129.474\)
Root analytic conductor: \(3.37323\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(2\)
Selberg data: \((4,\ 2030625,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad3$C_1$ \( ( 1 + T )^{2} \)
5 \( 1 \)
19$C_1$ \( ( 1 + T )^{2} \)
good2$D_{4}$ \( 1 - T + 3 T^{2} - p T^{3} + p^{2} T^{4} \) 2.2.ab_d
7$C_2^2$ \( 1 + 9 T^{2} + p^{2} T^{4} \) 2.7.a_j
11$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.11.i_bm
13$D_{4}$ \( 1 - 4 T + 10 T^{2} - 4 p T^{3} + p^{2} T^{4} \) 2.13.ae_k
17$D_{4}$ \( 1 + 2 T + 30 T^{2} + 2 p T^{3} + p^{2} T^{4} \) 2.17.c_be
23$D_{4}$ \( 1 - 2 T + 42 T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.23.ac_bq
29$D_{4}$ \( 1 - 6 T + 47 T^{2} - 6 p T^{3} + p^{2} T^{4} \) 2.29.ag_bv
31$D_{4}$ \( 1 + 12 T + 78 T^{2} + 12 p T^{3} + p^{2} T^{4} \) 2.31.m_da
37$D_{4}$ \( 1 - 10 T + 94 T^{2} - 10 p T^{3} + p^{2} T^{4} \) 2.37.ak_dq
41$C_2$ \( ( 1 + 5 T + p T^{2} )^{2} \) 2.41.k_ed
43$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.43.ai_dy
47$D_{4}$ \( 1 + 8 T + 90 T^{2} + 8 p T^{3} + p^{2} T^{4} \) 2.47.i_dm
53$C_2$ \( ( 1 + 5 T + p T^{2} )^{2} \) 2.53.k_fb
59$D_{4}$ \( 1 + 16 T + 137 T^{2} + 16 p T^{3} + p^{2} T^{4} \) 2.59.q_fh
61$D_{4}$ \( 1 + 2 T + 43 T^{2} + 2 p T^{3} + p^{2} T^{4} \) 2.61.c_br
67$D_{4}$ \( 1 + 4 T + 58 T^{2} + 4 p T^{3} + p^{2} T^{4} \) 2.67.e_cg
71$D_{4}$ \( 1 + 4 T + 21 T^{2} + 4 p T^{3} + p^{2} T^{4} \) 2.71.e_v
73$D_{4}$ \( 1 + 2 T + 127 T^{2} + 2 p T^{3} + p^{2} T^{4} \) 2.73.c_ex
79$D_{4}$ \( 1 + 18 T + 194 T^{2} + 18 p T^{3} + p^{2} T^{4} \) 2.79.s_hm
83$D_{4}$ \( 1 - 4 T + 90 T^{2} - 4 p T^{3} + p^{2} T^{4} \) 2.83.ae_dm
89$D_{4}$ \( 1 + 2 T + 99 T^{2} + 2 p T^{3} + p^{2} T^{4} \) 2.89.c_dv
97$D_{4}$ \( 1 - 10 T + 174 T^{2} - 10 p T^{3} + p^{2} T^{4} \) 2.97.ak_gs
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

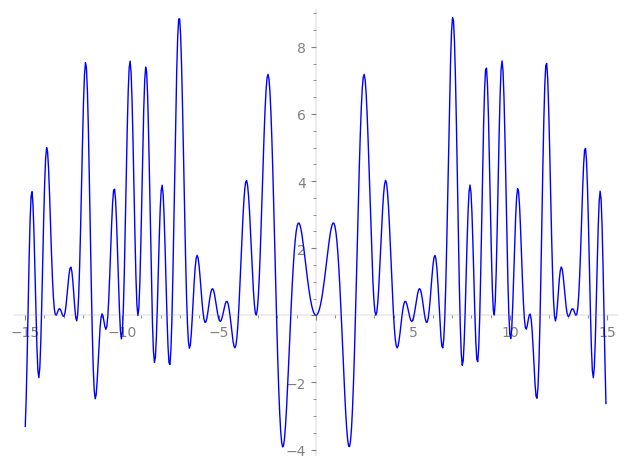
Imaginary part of the first few zeros on the critical line

−9.176153345810089195109099619179, −9.157254998676814988792378069843, −8.432102929509929922275826134838, −8.182100186952644210441619611509, −7.67482742530379919124468012861, −7.41471479208256770286099426016, −6.63533759922414518451996517384, −6.36538952888212725836048387460, −5.79875506410425517316478877992, −5.59286474429441944587828071313, −5.04838999753988597928240169900, −4.80528437808611238033786336830, −4.42932977323753465386587912750, −3.99274633237036053211251197976, −3.08920563746680637515058445191, −3.07925704714927071627180892721, −2.03321221382181056788308769045, −1.29945837987532816130365031028, 0, 0, 1.29945837987532816130365031028, 2.03321221382181056788308769045, 3.07925704714927071627180892721, 3.08920563746680637515058445191, 3.99274633237036053211251197976, 4.42932977323753465386587912750, 4.80528437808611238033786336830, 5.04838999753988597928240169900, 5.59286474429441944587828071313, 5.79875506410425517316478877992, 6.36538952888212725836048387460, 6.63533759922414518451996517384, 7.41471479208256770286099426016, 7.67482742530379919124468012861, 8.182100186952644210441619611509, 8.432102929509929922275826134838, 9.157254998676814988792378069843, 9.176153345810089195109099619179

Graph of the $Z$-function along the critical line