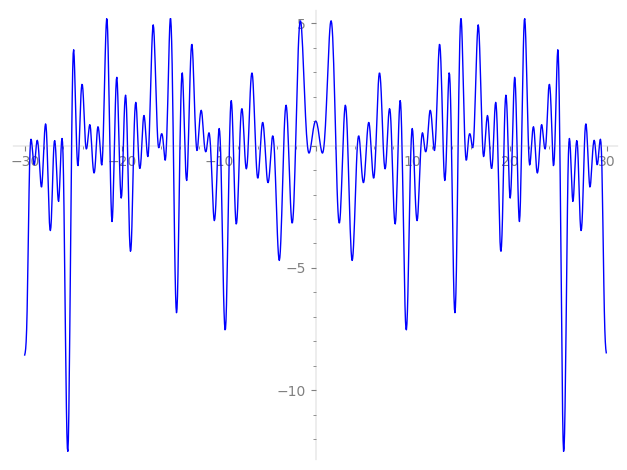
| L(s) = 1 | − 2·3-s − 2·5-s + 9-s − 4·11-s + 4·15-s − 6·17-s + 8·19-s + 23-s − 25-s + 4·27-s + 2·29-s + 6·31-s + 8·33-s + 2·37-s + 8·43-s − 2·45-s + 2·47-s + 12·51-s + 6·53-s + 8·55-s − 16·57-s − 6·59-s + 10·61-s + 12·67-s − 2·69-s − 16·71-s − 4·73-s + ⋯ |
| L(s) = 1 | − 1.15·3-s − 0.894·5-s + 1/3·9-s − 1.20·11-s + 1.03·15-s − 1.45·17-s + 1.83·19-s + 0.208·23-s − 1/5·25-s + 0.769·27-s + 0.371·29-s + 1.07·31-s + 1.39·33-s + 0.328·37-s + 1.21·43-s − 0.298·45-s + 0.291·47-s + 1.68·51-s + 0.824·53-s + 1.07·55-s − 2.11·57-s − 0.781·59-s + 1.28·61-s + 1.46·67-s − 0.240·69-s − 1.89·71-s − 0.468·73-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 72128 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 72128 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.003597486\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.003597486\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 \) | |
| 7 | \( 1 \) | |
| 23 | \( 1 - T \) | |
| good | 3 | \( 1 + 2 T + p T^{2} \) | 1.3.c |
| 5 | \( 1 + 2 T + p T^{2} \) | 1.5.c |
| 11 | \( 1 + 4 T + p T^{2} \) | 1.11.e |
| 13 | \( 1 + p T^{2} \) | 1.13.a |
| 17 | \( 1 + 6 T + p T^{2} \) | 1.17.g |
| 19 | \( 1 - 8 T + p T^{2} \) | 1.19.ai |
| 29 | \( 1 - 2 T + p T^{2} \) | 1.29.ac |
| 31 | \( 1 - 6 T + p T^{2} \) | 1.31.ag |
| 37 | \( 1 - 2 T + p T^{2} \) | 1.37.ac |
| 41 | \( 1 + p T^{2} \) | 1.41.a |
| 43 | \( 1 - 8 T + p T^{2} \) | 1.43.ai |
| 47 | \( 1 - 2 T + p T^{2} \) | 1.47.ac |
| 53 | \( 1 - 6 T + p T^{2} \) | 1.53.ag |
| 59 | \( 1 + 6 T + p T^{2} \) | 1.59.g |
| 61 | \( 1 - 10 T + p T^{2} \) | 1.61.ak |
| 67 | \( 1 - 12 T + p T^{2} \) | 1.67.am |
| 71 | \( 1 + 16 T + p T^{2} \) | 1.71.q |
| 73 | \( 1 + 4 T + p T^{2} \) | 1.73.e |
| 79 | \( 1 - 4 T + p T^{2} \) | 1.79.ae |
| 83 | \( 1 + 4 T + p T^{2} \) | 1.83.e |
| 89 | \( 1 - 2 T + p T^{2} \) | 1.89.ac |
| 97 | \( 1 + 2 T + p T^{2} \) | 1.97.c |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−13.99421033701690, −13.49618087977266, −13.13388523885791, −12.31851801092489, −12.14520286611404, −11.47288947761235, −11.20100056611863, −10.84499564956781, −10.07943296993695, −9.820851317788303, −8.896088459740602, −8.496809076823110, −7.841771629558086, −7.350408339596169, −6.958065208170948, −6.205830574336918, −5.695167237400600, −5.231406416802693, −4.569389720082254, −4.292133792641387, −3.300755984785524, −2.809114738458444, −2.076684416112158, −0.8561313586426749, −0.4892144114788938,
0.4892144114788938, 0.8561313586426749, 2.076684416112158, 2.809114738458444, 3.300755984785524, 4.292133792641387, 4.569389720082254, 5.231406416802693, 5.695167237400600, 6.205830574336918, 6.958065208170948, 7.350408339596169, 7.841771629558086, 8.496809076823110, 8.896088459740602, 9.820851317788303, 10.07943296993695, 10.84499564956781, 11.20100056611863, 11.47288947761235, 12.14520286611404, 12.31851801092489, 13.13388523885791, 13.49618087977266, 13.99421033701690