| L(s) = 1 | − 2-s + 3-s + 4-s + 5-s − 6-s − 4·7-s − 8-s + 9-s − 10-s − 11-s + 12-s + 2·13-s + 4·14-s + 15-s + 16-s + 2·17-s − 18-s − 8·19-s + 20-s − 4·21-s + 22-s − 24-s + 25-s − 2·26-s + 27-s − 4·28-s − 2·29-s + ⋯ |
| L(s) = 1 | − 0.707·2-s + 0.577·3-s + 1/2·4-s + 0.447·5-s − 0.408·6-s − 1.51·7-s − 0.353·8-s + 1/3·9-s − 0.316·10-s − 0.301·11-s + 0.288·12-s + 0.554·13-s + 1.06·14-s + 0.258·15-s + 1/4·16-s + 0.485·17-s − 0.235·18-s − 1.83·19-s + 0.223·20-s − 0.872·21-s + 0.213·22-s − 0.204·24-s + 1/5·25-s − 0.392·26-s + 0.192·27-s − 0.755·28-s − 0.371·29-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 317130 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 317130 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 + T \) | |
| 3 | \( 1 - T \) | |
| 5 | \( 1 - T \) | |
| 11 | \( 1 + T \) | |
| 31 | \( 1 \) | |
| good | 7 | \( 1 + 4 T + p T^{2} \) | 1.7.e |
| 13 | \( 1 - 2 T + p T^{2} \) | 1.13.ac |
| 17 | \( 1 - 2 T + p T^{2} \) | 1.17.ac |
| 19 | \( 1 + 8 T + p T^{2} \) | 1.19.i |
| 23 | \( 1 + p T^{2} \) | 1.23.a |
| 29 | \( 1 + 2 T + p T^{2} \) | 1.29.c |
| 37 | \( 1 - 10 T + p T^{2} \) | 1.37.ak |
| 41 | \( 1 + 10 T + p T^{2} \) | 1.41.k |
| 43 | \( 1 + p T^{2} \) | 1.43.a |
| 47 | \( 1 + p T^{2} \) | 1.47.a |
| 53 | \( 1 + 14 T + p T^{2} \) | 1.53.o |
| 59 | \( 1 + 4 T + p T^{2} \) | 1.59.e |
| 61 | \( 1 + 14 T + p T^{2} \) | 1.61.o |
| 67 | \( 1 + 4 T + p T^{2} \) | 1.67.e |
| 71 | \( 1 - 8 T + p T^{2} \) | 1.71.ai |
| 73 | \( 1 + 10 T + p T^{2} \) | 1.73.k |
| 79 | \( 1 + 12 T + p T^{2} \) | 1.79.m |
| 83 | \( 1 + 4 T + p T^{2} \) | 1.83.e |
| 89 | \( 1 - 6 T + p T^{2} \) | 1.89.ag |
| 97 | \( 1 + 14 T + p T^{2} \) | 1.97.o |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
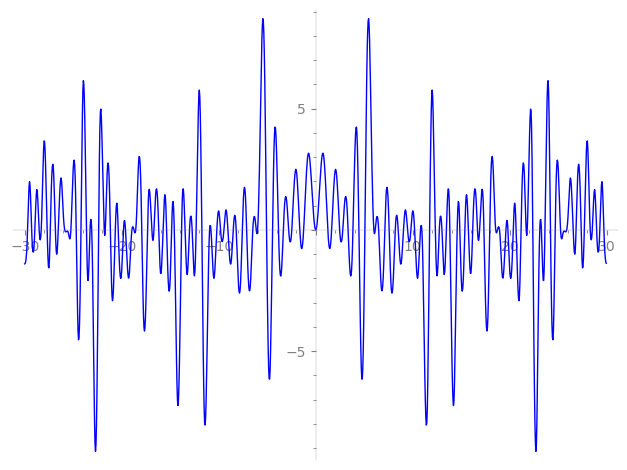
Imaginary part of the first few zeros on the critical line
−13.00909976566022, −12.74054971198543, −12.32258334243043, −11.73687066676511, −10.94393470886038, −10.79398961215492, −10.19925948796804, −9.811169682442102, −9.466253127832681, −9.045094277213509, −8.504631058785228, −8.199906299101817, −7.569923559334671, −7.119922480454714, −6.489350193558083, −6.137741736817775, −5.992510466044484, −5.069011263519043, −4.453403550302844, −3.839750494901109, −3.337674379864069, −2.791626921216447, −2.467809398991875, −1.640769462370860, −1.243041093185176, 0, 0,
1.243041093185176, 1.640769462370860, 2.467809398991875, 2.791626921216447, 3.337674379864069, 3.839750494901109, 4.453403550302844, 5.069011263519043, 5.992510466044484, 6.137741736817775, 6.489350193558083, 7.119922480454714, 7.569923559334671, 8.199906299101817, 8.504631058785228, 9.045094277213509, 9.466253127832681, 9.811169682442102, 10.19925948796804, 10.79398961215492, 10.94393470886038, 11.73687066676511, 12.32258334243043, 12.74054971198543, 13.00909976566022