| L(s) = 1 | − 2·4-s − 7-s + 2·13-s + 4·16-s − 6·17-s + 7·19-s − 6·23-s + 2·28-s − 31-s + 7·37-s − 6·41-s + 8·43-s − 6·49-s − 4·52-s − 6·53-s + 12·59-s + 61-s − 8·64-s + 7·67-s + 12·68-s − 6·71-s − 13·73-s − 14·76-s − 11·79-s + 18·89-s − 2·91-s + 12·92-s + ⋯ |
| L(s) = 1 | − 4-s − 0.377·7-s + 0.554·13-s + 16-s − 1.45·17-s + 1.60·19-s − 1.25·23-s + 0.377·28-s − 0.179·31-s + 1.15·37-s − 0.937·41-s + 1.21·43-s − 6/7·49-s − 0.554·52-s − 0.824·53-s + 1.56·59-s + 0.128·61-s − 64-s + 0.855·67-s + 1.45·68-s − 0.712·71-s − 1.52·73-s − 1.60·76-s − 1.23·79-s + 1.90·89-s − 0.209·91-s + 1.25·92-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 27225 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 27225 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 3 | \( 1 \) | |
| 5 | \( 1 \) | |
| 11 | \( 1 \) | |
| good | 2 | \( 1 + p T^{2} \) | 1.2.a |
| 7 | \( 1 + T + p T^{2} \) | 1.7.b |
| 13 | \( 1 - 2 T + p T^{2} \) | 1.13.ac |
| 17 | \( 1 + 6 T + p T^{2} \) | 1.17.g |
| 19 | \( 1 - 7 T + p T^{2} \) | 1.19.ah |
| 23 | \( 1 + 6 T + p T^{2} \) | 1.23.g |
| 29 | \( 1 + p T^{2} \) | 1.29.a |
| 31 | \( 1 + T + p T^{2} \) | 1.31.b |
| 37 | \( 1 - 7 T + p T^{2} \) | 1.37.ah |
| 41 | \( 1 + 6 T + p T^{2} \) | 1.41.g |
| 43 | \( 1 - 8 T + p T^{2} \) | 1.43.ai |
| 47 | \( 1 + p T^{2} \) | 1.47.a |
| 53 | \( 1 + 6 T + p T^{2} \) | 1.53.g |
| 59 | \( 1 - 12 T + p T^{2} \) | 1.59.am |
| 61 | \( 1 - T + p T^{2} \) | 1.61.ab |
| 67 | \( 1 - 7 T + p T^{2} \) | 1.67.ah |
| 71 | \( 1 + 6 T + p T^{2} \) | 1.71.g |
| 73 | \( 1 + 13 T + p T^{2} \) | 1.73.n |
| 79 | \( 1 + 11 T + p T^{2} \) | 1.79.l |
| 83 | \( 1 + p T^{2} \) | 1.83.a |
| 89 | \( 1 - 18 T + p T^{2} \) | 1.89.as |
| 97 | \( 1 - T + p T^{2} \) | 1.97.ab |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
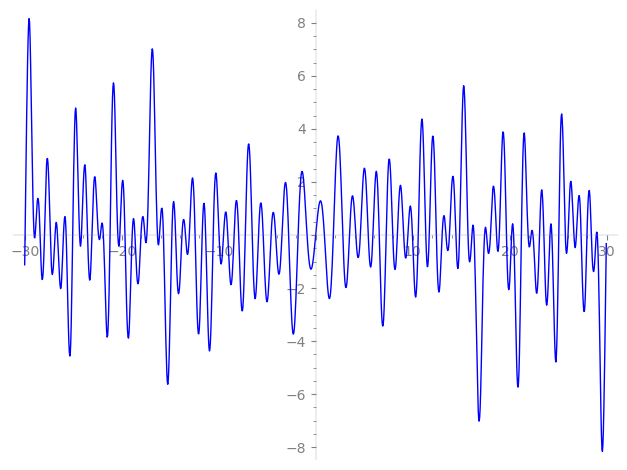
Imaginary part of the first few zeros on the critical line
−15.69705289085765, −14.82741953079423, −14.44492549035837, −13.78534377273250, −13.42607513796416, −13.02704994969815, −12.43308735341442, −11.70473749464523, −11.34375571026129, −10.56848972639650, −9.972915114395134, −9.501885903320510, −9.065264819050335, −8.414559908481644, −7.940249082623094, −7.261810359606210, −6.547862296016837, −5.895423627456064, −5.415297817270274, −4.600016856440417, −4.134159268042565, −3.480179437028206, −2.790823427094901, −1.815042792053256, −0.8948897220423774, 0,
0.8948897220423774, 1.815042792053256, 2.790823427094901, 3.480179437028206, 4.134159268042565, 4.600016856440417, 5.415297817270274, 5.895423627456064, 6.547862296016837, 7.261810359606210, 7.940249082623094, 8.414559908481644, 9.065264819050335, 9.501885903320510, 9.972915114395134, 10.56848972639650, 11.34375571026129, 11.70473749464523, 12.43308735341442, 13.02704994969815, 13.42607513796416, 13.78534377273250, 14.44492549035837, 14.82741953079423, 15.69705289085765