↑

Properties

Label 4-640332-1.1-c1e2-0-20
Degree $4$
Conductor $640332$
Sign $1$
Analytic cond. $40.8281$
Root an. cond. $2.52778$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 3-s + 4-s + 8·5-s − 2·7-s + 9-s − 12-s − 8·15-s + 16-s + 4·17-s + 8·20-s + 2·21-s + 38·25-s − 27-s − 2·28-s − 16·35-s + 36-s − 4·37-s − 4·41-s + 8·43-s + 8·45-s + 4·47-s − 48-s − 3·49-s − 4·51-s − 8·60-s − 2·63-s + 64-s + ⋯
L(s)  = 1  − 0.577·3-s + 1/2·4-s + 3.57·5-s − 0.755·7-s + 1/3·9-s − 0.288·12-s − 2.06·15-s + 1/4·16-s + 0.970·17-s + 1.78·20-s + 0.436·21-s + 38/5·25-s − 0.192·27-s − 0.377·28-s − 2.70·35-s + 1/6·36-s − 0.657·37-s − 0.624·41-s + 1.21·43-s + 1.19·45-s + 0.583·47-s − 0.144·48-s − 3/7·49-s − 0.560·51-s − 1.03·60-s − 0.251·63-s + 1/8·64-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 640332 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 640332 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(640332\)    =    \(2^{2} \cdot 3^{3} \cdot 7^{2} \cdot 11^{2}\)
Sign: $1$
Analytic conductor: \(40.8281\)
Root analytic conductor: \(2.52778\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 640332,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(3.858641056\)
\(L(\frac12)\) \(\approx\) \(3.858641056\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
3$C_1$ \( 1 + T \)
7$C_2$ \( 1 + 2 T + p T^{2} \)
11$C_1$$\times$$C_1$ \( ( 1 - T )( 1 + T ) \)
good5$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.5.ai_ba
13$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.13.a_k
17$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.17.ae_bm
19$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.19.a_bm
23$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.23.a_k
29$C_2$ \( ( 1 - 10 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.29.a_abq
31$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.31.a_ac
37$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.37.e_da
41$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.41.e_di
43$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.43.ai_dy
47$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.47.ae_du
53$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.53.a_dm
59$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.59.a_eo
61$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) 2.61.a_cg
67$C_2$ \( ( 1 + 12 T + p T^{2} )^{2} \) 2.67.y_ks
71$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.71.a_fi
73$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.73.a_eg
79$C_2$ \( ( 1 - 10 T + p T^{2} )^{2} \) 2.79.au_jy
83$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.83.i_ha
89$C_2$ \( ( 1 + 10 T + p T^{2} )^{2} \) 2.89.u_ks
97$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) 2.97.a_hi
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

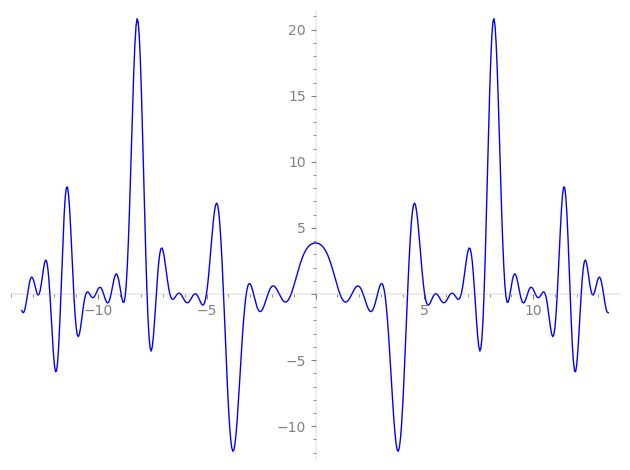
Imaginary part of the first few zeros on the critical line

−8.734399327056068821213499579504, −7.74249612429138712743707138359, −7.31626404793277731789533693062, −6.69373326676767816887250497086, −6.35062410158064670794655966913, −6.20004880727144301320499647411, −5.56849277330524351488966193226, −5.48462700120923997068508135767, −5.01244554431640501263959251141, −4.22775784486927931972933466181, −3.18510621994423060681354856306, −2.84811781912171505509456779453, −2.18727745386797108535245912439, −1.66815280525216283373919758824, −1.12176628667720465571658579928, 1.12176628667720465571658579928, 1.66815280525216283373919758824, 2.18727745386797108535245912439, 2.84811781912171505509456779453, 3.18510621994423060681354856306, 4.22775784486927931972933466181, 5.01244554431640501263959251141, 5.48462700120923997068508135767, 5.56849277330524351488966193226, 6.20004880727144301320499647411, 6.35062410158064670794655966913, 6.69373326676767816887250497086, 7.31626404793277731789533693062, 7.74249612429138712743707138359, 8.734399327056068821213499579504

Graph of the $Z$-function along the critical line