↑

Properties

Label 4-4080e2-1.1-c1e2-0-3
Degree $4$
Conductor $16646400$
Sign $1$
Analytic cond. $1061.38$
Root an. cond. $5.70779$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 4·5-s − 9-s − 4·11-s − 8·19-s + 11·25-s − 16·29-s − 8·41-s − 4·45-s − 2·49-s − 16·55-s + 4·61-s − 28·71-s + 8·79-s + 81-s + 12·89-s − 32·95-s + 4·99-s − 12·101-s + 12·109-s − 10·121-s + 24·125-s + 127-s + 131-s + 137-s + 139-s − 64·145-s + 149-s + ⋯
L(s)  = 1  + 1.78·5-s − 1/3·9-s − 1.20·11-s − 1.83·19-s + 11/5·25-s − 2.97·29-s − 1.24·41-s − 0.596·45-s − 2/7·49-s − 2.15·55-s + 0.512·61-s − 3.32·71-s + 0.900·79-s + 1/9·81-s + 1.27·89-s − 3.28·95-s + 0.402·99-s − 1.19·101-s + 1.14·109-s − 0.909·121-s + 2.14·125-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s − 5.31·145-s + 0.0819·149-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 16646400 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 16646400 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(16646400\)    =    \(2^{8} \cdot 3^{2} \cdot 5^{2} \cdot 17^{2}\)
Sign: $1$
Analytic conductor: \(1061.38\)
Root analytic conductor: \(5.70779\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 16646400,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(0.8124226157\)
\(L(\frac12)\) \(\approx\) \(0.8124226157\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2 \( 1 \)
3$C_2$ \( 1 + T^{2} \)
5$C_2$ \( 1 - 4 T + p T^{2} \)
17$C_2$ \( 1 + T^{2} \)
good7$C_2^2$ \( 1 + 2 T^{2} + p^{2} T^{4} \) 2.7.a_c
11$C_2$ \( ( 1 + 2 T + p T^{2} )^{2} \) 2.11.e_ba
13$C_2$ \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) 2.13.a_ak
19$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.19.i_cc
23$C_2^2$ \( 1 + 18 T^{2} + p^{2} T^{4} \) 2.23.a_s
29$C_2$ \( ( 1 + 8 T + p T^{2} )^{2} \) 2.29.q_es
31$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.31.a_ck
37$C_2$ \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) 2.37.a_acs
41$C_2$ \( ( 1 + 4 T + p T^{2} )^{2} \) 2.41.i_du
43$C_2^2$ \( 1 - 50 T^{2} + p^{2} T^{4} \) 2.43.a_aby
47$C_2^2$ \( 1 + 50 T^{2} + p^{2} T^{4} \) 2.47.a_by
53$C_2$ \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.53.a_dm
59$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.59.a_eo
61$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.61.ae_ew
67$C_2^2$ \( 1 - 130 T^{2} + p^{2} T^{4} \) 2.67.a_afa
71$C_2$ \( ( 1 + 14 T + p T^{2} )^{2} \) 2.71.bc_na
73$C_2^2$ \( 1 - 142 T^{2} + p^{2} T^{4} \) 2.73.a_afm
79$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.79.ai_gs
83$C_2^2$ \( 1 + 90 T^{2} + p^{2} T^{4} \) 2.83.a_dm
89$C_2$ \( ( 1 - 6 T + p T^{2} )^{2} \) 2.89.am_ig
97$C_2^2$ \( 1 + 2 T^{2} + p^{2} T^{4} \) 2.97.a_c
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

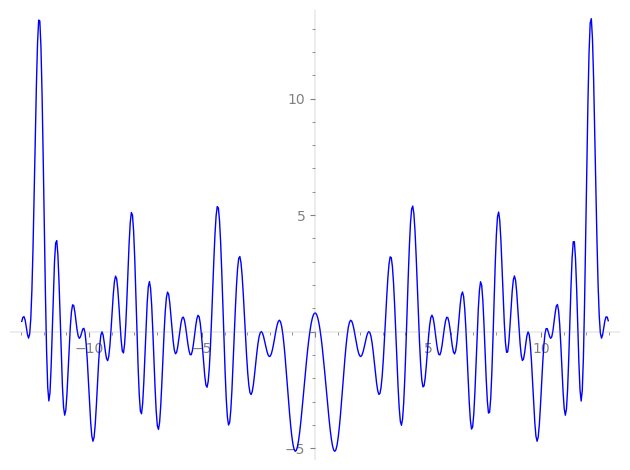
Imaginary part of the first few zeros on the critical line

−9.033805571326485220776066468610, −8.391766661146222979146243924709, −7.87908325224236674445370870054, −7.48656804435424140106639391647, −7.17722036182747735212216589319, −6.67837585847243828092457067607, −6.31791755509226671748118546615, −5.98818002603226774207718428429, −5.69755229040930681405156972580, −5.31389913408285740157837546032, −5.03970695130580699538981306540, −4.60132678322873577446396199695, −4.04162934722050316635304336416, −3.56987602628174528629380106109, −3.08828724626126866996927262036, −2.40430825028022819867698866586, −2.36037573143299676521277237975, −1.74129312462801483025330061617, −1.44012973547861501395924901937, −0.23210680810937249948008611811, 0.23210680810937249948008611811, 1.44012973547861501395924901937, 1.74129312462801483025330061617, 2.36037573143299676521277237975, 2.40430825028022819867698866586, 3.08828724626126866996927262036, 3.56987602628174528629380106109, 4.04162934722050316635304336416, 4.60132678322873577446396199695, 5.03970695130580699538981306540, 5.31389913408285740157837546032, 5.69755229040930681405156972580, 5.98818002603226774207718428429, 6.31791755509226671748118546615, 6.67837585847243828092457067607, 7.17722036182747735212216589319, 7.48656804435424140106639391647, 7.87908325224236674445370870054, 8.391766661146222979146243924709, 9.033805571326485220776066468610

Graph of the $Z$-function along the critical line