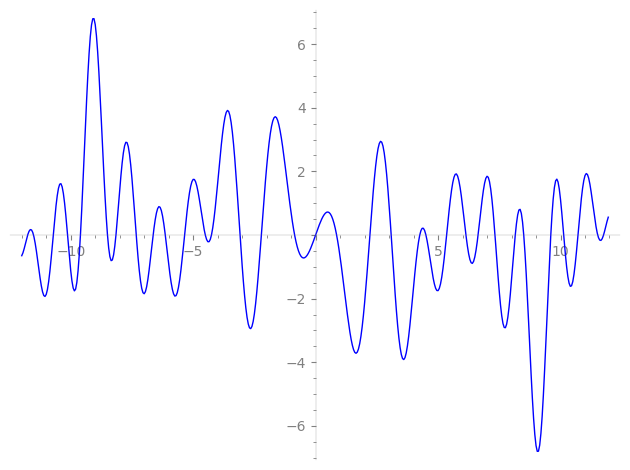
| L(s) = 1 | − 2·3-s − 2·5-s + 9-s + 11-s − 4·13-s + 4·15-s − 4·19-s − 4·23-s − 25-s + 4·27-s + 10·29-s + 2·31-s − 2·33-s + 10·37-s + 8·39-s − 4·43-s − 2·45-s − 2·47-s + 2·53-s − 2·55-s + 8·57-s + 6·59-s + 8·65-s + 8·67-s + 8·69-s − 12·71-s + 12·73-s + ⋯ |
| L(s) = 1 | − 1.15·3-s − 0.894·5-s + 1/3·9-s + 0.301·11-s − 1.10·13-s + 1.03·15-s − 0.917·19-s − 0.834·23-s − 1/5·25-s + 0.769·27-s + 1.85·29-s + 0.359·31-s − 0.348·33-s + 1.64·37-s + 1.28·39-s − 0.609·43-s − 0.298·45-s − 0.291·47-s + 0.274·53-s − 0.269·55-s + 1.05·57-s + 0.781·59-s + 0.992·65-s + 0.977·67-s + 0.963·69-s − 1.42·71-s + 1.40·73-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 8624 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 8624 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 \) | |
| 7 | \( 1 \) | |
| 11 | \( 1 - T \) | |
| good | 3 | \( 1 + 2 T + p T^{2} \) | 1.3.c |
| 5 | \( 1 + 2 T + p T^{2} \) | 1.5.c |
| 13 | \( 1 + 4 T + p T^{2} \) | 1.13.e |
| 17 | \( 1 + p T^{2} \) | 1.17.a |
| 19 | \( 1 + 4 T + p T^{2} \) | 1.19.e |
| 23 | \( 1 + 4 T + p T^{2} \) | 1.23.e |
| 29 | \( 1 - 10 T + p T^{2} \) | 1.29.ak |
| 31 | \( 1 - 2 T + p T^{2} \) | 1.31.ac |
| 37 | \( 1 - 10 T + p T^{2} \) | 1.37.ak |
| 41 | \( 1 + p T^{2} \) | 1.41.a |
| 43 | \( 1 + 4 T + p T^{2} \) | 1.43.e |
| 47 | \( 1 + 2 T + p T^{2} \) | 1.47.c |
| 53 | \( 1 - 2 T + p T^{2} \) | 1.53.ac |
| 59 | \( 1 - 6 T + p T^{2} \) | 1.59.ag |
| 61 | \( 1 + p T^{2} \) | 1.61.a |
| 67 | \( 1 - 8 T + p T^{2} \) | 1.67.ai |
| 71 | \( 1 + 12 T + p T^{2} \) | 1.71.m |
| 73 | \( 1 - 12 T + p T^{2} \) | 1.73.am |
| 79 | \( 1 + 16 T + p T^{2} \) | 1.79.q |
| 83 | \( 1 + 4 T + p T^{2} \) | 1.83.e |
| 89 | \( 1 - 6 T + p T^{2} \) | 1.89.ag |
| 97 | \( 1 - 10 T + p T^{2} \) | 1.97.ak |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−7.32420508778679005054827500490, −6.63389363769639516874915074692, −6.13863232188018401440349319825, −5.34961543116429007897252188097, −4.50410021803085905518670644522, −4.25267031441684714845495523103, −3.08557065446550481726612453349, −2.21593463041099287027782326347, −0.857071651185432583891932144181, 0,
0.857071651185432583891932144181, 2.21593463041099287027782326347, 3.08557065446550481726612453349, 4.25267031441684714845495523103, 4.50410021803085905518670644522, 5.34961543116429007897252188097, 6.13863232188018401440349319825, 6.63389363769639516874915074692, 7.32420508778679005054827500490