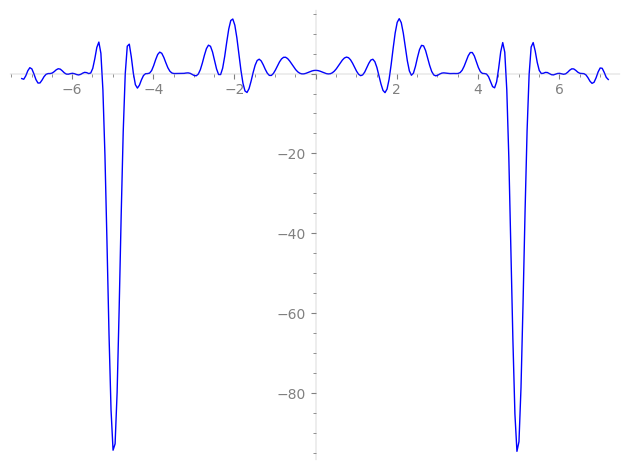
| L(s) = 1 | − 12·7-s + 12·13-s − 16·31-s + 12·37-s + 72·49-s − 40·61-s + 24·67-s − 24·73-s − 144·91-s − 48·97-s + 12·103-s + 8·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 72·169-s + 173-s + 179-s + 181-s + 191-s + 193-s + ⋯ |
| L(s) = 1 | − 4.53·7-s + 3.32·13-s − 2.87·31-s + 1.97·37-s + 72/7·49-s − 5.12·61-s + 2.93·67-s − 2.80·73-s − 15.0·91-s − 4.87·97-s + 1.18·103-s + 8/11·121-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s + 5.53·169-s + 0.0760·173-s + 0.0747·179-s + 0.0743·181-s + 0.0723·191-s + 0.0719·193-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{8} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{8} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(0.8039676043\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.8039676043\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | | \( 1 \) |
| 5 | | \( 1 \) |
| good | 7 | $C_2^2$ | \( ( 1 + 6 T + 18 T^{2} + 6 p T^{3} + p^{2} T^{4} )^{2} \) |
| 11 | $C_2^2$ | \( ( 1 - 4 T^{2} + p^{2} T^{4} )^{2} \) |
| 13 | $C_2^2$ | \( ( 1 - 6 T + 18 T^{2} - 6 p T^{3} + p^{2} T^{4} )^{2} \) |
| 17 | $C_2^2$$\times$$C_2^2$ | \( ( 1 - 8 T + 32 T^{2} - 8 p T^{3} + p^{2} T^{4} )( 1 + 8 T + 32 T^{2} + 8 p T^{3} + p^{2} T^{4} ) \) |
| 19 | $C_2^2$ | \( ( 1 - 34 T^{2} + p^{2} T^{4} )^{2} \) |
| 23 | $C_2^3$ | \( 1 - 958 T^{4} + p^{4} T^{8} \) |
| 29 | $C_2^2$ | \( ( 1 - 14 T^{2} + p^{2} T^{4} )^{2} \) |
| 31 | $C_2$ | \( ( 1 + 4 T + p T^{2} )^{4} \) |
| 37 | $C_2^2$ | \( ( 1 - 6 T + 18 T^{2} - 6 p T^{3} + p^{2} T^{4} )^{2} \) |
| 41 | $C_2^2$ | \( ( 1 - 64 T^{2} + p^{2} T^{4} )^{2} \) |
| 43 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) |
| 47 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) |
| 53 | $C_2^3$ | \( 1 - 718 T^{4} + p^{4} T^{8} \) |
| 59 | $C_2^2$ | \( ( 1 + 100 T^{2} + p^{2} T^{4} )^{2} \) |
| 61 | $C_2$ | \( ( 1 + 10 T + p T^{2} )^{4} \) |
| 67 | $C_2^2$ | \( ( 1 - 12 T + 72 T^{2} - 12 p T^{3} + p^{2} T^{4} )^{2} \) |
| 71 | $C_2^2$ | \( ( 1 - 70 T^{2} + p^{2} T^{4} )^{2} \) |
| 73 | $C_2^2$ | \( ( 1 + 12 T + 72 T^{2} + 12 p T^{3} + p^{2} T^{4} )^{2} \) |
| 79 | $C_2^2$ | \( ( 1 - 94 T^{2} + p^{2} T^{4} )^{2} \) |
| 83 | $C_2^3$ | \( 1 - 13294 T^{4} + p^{4} T^{8} \) |
| 89 | $C_2^2$ | \( ( 1 + 160 T^{2} + p^{2} T^{4} )^{2} \) |
| 97 | $C_2^2$ | \( ( 1 + 24 T + 288 T^{2} + 24 p T^{3} + p^{2} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.03473042237495144621308017495, −5.95256564120066370374611085745, −5.75558297183047096944225033957, −5.59213432417678247641882442632, −5.56007453510609837644358181349, −5.25962441247281279768044072756, −4.69124011330928282868153434227, −4.49094671668635153751562382170, −4.16818931835725914330796384609, −4.16315258870946924964138343780, −4.11958685994604004113776454038, −3.48595518769171527377832087961, −3.46098288926514858444963316548, −3.33497932430606527719270284912, −3.29081622052368154128938704795, −3.07883392893344937281941627016, −2.88384843612869010975269940427, −2.40437625701750293633448439995, −2.32930855091232554955624394137, −1.83019518314440161562468013050, −1.54696649434673458057833081646, −1.18589448204946154992609576603, −1.04328289901329186633149598742, −0.37354978367190858733900814616, −0.25721827161045908538251413320,
0.25721827161045908538251413320, 0.37354978367190858733900814616, 1.04328289901329186633149598742, 1.18589448204946154992609576603, 1.54696649434673458057833081646, 1.83019518314440161562468013050, 2.32930855091232554955624394137, 2.40437625701750293633448439995, 2.88384843612869010975269940427, 3.07883392893344937281941627016, 3.29081622052368154128938704795, 3.33497932430606527719270284912, 3.46098288926514858444963316548, 3.48595518769171527377832087961, 4.11958685994604004113776454038, 4.16315258870946924964138343780, 4.16818931835725914330796384609, 4.49094671668635153751562382170, 4.69124011330928282868153434227, 5.25962441247281279768044072756, 5.56007453510609837644358181349, 5.59213432417678247641882442632, 5.75558297183047096944225033957, 5.95256564120066370374611085745, 6.03473042237495144621308017495