| L(s) = 1 | + 5·3-s + 3·5-s + 5·7-s + 8·9-s + 5·11-s + 5·13-s + 15·15-s + 4·17-s + 7·19-s + 25·21-s + 4·23-s − 7·25-s + 27-s − 3·29-s − 2·31-s + 25·33-s + 15·35-s + 37-s + 25·39-s − 7·41-s + 15·43-s + 24·45-s − 6·47-s + 15·49-s + 20·51-s − 11·53-s + 15·55-s + ⋯ |
| L(s) = 1 | + 2.88·3-s + 1.34·5-s + 1.88·7-s + 8/3·9-s + 1.50·11-s + 1.38·13-s + 3.87·15-s + 0.970·17-s + 1.60·19-s + 5.45·21-s + 0.834·23-s − 7/5·25-s + 0.192·27-s − 0.557·29-s − 0.359·31-s + 4.35·33-s + 2.53·35-s + 0.164·37-s + 4.00·39-s − 1.09·41-s + 2.28·43-s + 3.57·45-s − 0.875·47-s + 15/7·49-s + 2.80·51-s − 1.51·53-s + 2.02·55-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{30} \cdot 7^{5} \cdot 13^{5}\right)^{s/2} \, \Gamma_{\C}(s)^{5} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{30} \cdot 7^{5} \cdot 13^{5}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{5} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(129.1515140\) |
| \(L(\frac12)\) |
\(\approx\) |
\(129.1515140\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | | \( 1 \) | |
| 7 | $C_1$ | \( ( 1 - T )^{5} \) | |
| 13 | $C_1$ | \( ( 1 - T )^{5} \) | |
| good | 3 | $C_2 \wr S_5$ | \( 1 - 5 T + 17 T^{2} - 46 T^{3} + 34 p T^{4} - 194 T^{5} + 34 p^{2} T^{6} - 46 p^{2} T^{7} + 17 p^{3} T^{8} - 5 p^{4} T^{9} + p^{5} T^{10} \) | 5.3.af_r_abu_dy_ahm |
| 5 | $C_2 \wr S_5$ | \( 1 - 3 T + 16 T^{2} - 41 T^{3} + p^{3} T^{4} - 276 T^{5} + p^{4} T^{6} - 41 p^{2} T^{7} + 16 p^{3} T^{8} - 3 p^{4} T^{9} + p^{5} T^{10} \) | 5.5.ad_q_abp_ev_akq |
| 11 | $C_2 \wr S_5$ | \( 1 - 5 T + 41 T^{2} - 16 p T^{3} + 818 T^{4} - 2694 T^{5} + 818 p T^{6} - 16 p^{3} T^{7} + 41 p^{3} T^{8} - 5 p^{4} T^{9} + p^{5} T^{10} \) | 5.11.af_bp_agu_bfm_adzq |
| 17 | $C_2 \wr S_5$ | \( 1 - 4 T + 65 T^{2} - 166 T^{3} + 106 p T^{4} - 3460 T^{5} + 106 p^{2} T^{6} - 166 p^{2} T^{7} + 65 p^{3} T^{8} - 4 p^{4} T^{9} + p^{5} T^{10} \) | 5.17.ae_cn_agk_cri_afdc |
| 19 | $C_2 \wr S_5$ | \( 1 - 7 T + 54 T^{2} - 213 T^{3} + 1223 T^{4} - 4056 T^{5} + 1223 p T^{6} - 213 p^{2} T^{7} + 54 p^{3} T^{8} - 7 p^{4} T^{9} + p^{5} T^{10} \) | 5.19.ah_cc_aif_bvb_agaa |
| 23 | $C_2 \wr S_5$ | \( 1 - 4 T + 81 T^{2} - 356 T^{3} + 3193 T^{4} - 11872 T^{5} + 3193 p T^{6} - 356 p^{2} T^{7} + 81 p^{3} T^{8} - 4 p^{4} T^{9} + p^{5} T^{10} \) | 5.23.ae_dd_ans_esv_aroq |
| 29 | $C_2 \wr S_5$ | \( 1 + 3 T + 78 T^{2} + 221 T^{3} + 3323 T^{4} + 7764 T^{5} + 3323 p T^{6} + 221 p^{2} T^{7} + 78 p^{3} T^{8} + 3 p^{4} T^{9} + p^{5} T^{10} \) | 5.29.d_da_in_exv_lmq |
| 31 | $C_2 \wr S_5$ | \( 1 + 2 T + 79 T^{2} + 232 T^{3} + 4031 T^{4} + 8652 T^{5} + 4031 p T^{6} + 232 p^{2} T^{7} + 79 p^{3} T^{8} + 2 p^{4} T^{9} + p^{5} T^{10} \) | 5.31.c_db_iy_fzb_muu |
| 37 | $C_2 \wr S_5$ | \( 1 - T + 61 T^{2} - 272 T^{3} + 3100 T^{4} - 9658 T^{5} + 3100 p T^{6} - 272 p^{2} T^{7} + 61 p^{3} T^{8} - p^{4} T^{9} + p^{5} T^{10} \) | 5.37.ab_cj_akm_epg_aohm |
| 41 | $C_2 \wr S_5$ | \( 1 + 7 T + 113 T^{2} + 828 T^{3} + 6774 T^{4} + 43418 T^{5} + 6774 p T^{6} + 828 p^{2} T^{7} + 113 p^{3} T^{8} + 7 p^{4} T^{9} + p^{5} T^{10} \) | 5.41.h_ej_bfw_kao_cmfy |
| 43 | $C_2 \wr S_5$ | \( 1 - 15 T + 202 T^{2} - 1745 T^{3} + 15113 T^{4} - 98600 T^{5} + 15113 p T^{6} - 1745 p^{2} T^{7} + 202 p^{3} T^{8} - 15 p^{4} T^{9} + p^{5} T^{10} \) | 5.43.ap_hu_acpd_wjh_afpwi |
| 47 | $C_2 \wr S_5$ | \( 1 + 6 T + 165 T^{2} + 712 T^{3} + 12675 T^{4} + 42372 T^{5} + 12675 p T^{6} + 712 p^{2} T^{7} + 165 p^{3} T^{8} + 6 p^{4} T^{9} + p^{5} T^{10} \) | 5.47.g_gj_bbk_stn_ckrs |
| 53 | $C_2 \wr S_5$ | \( 1 + 11 T + 98 T^{2} + 869 T^{3} + 8831 T^{4} + 72308 T^{5} + 8831 p T^{6} + 869 p^{2} T^{7} + 98 p^{3} T^{8} + 11 p^{4} T^{9} + p^{5} T^{10} \) | 5.53.l_du_bhl_nbr_eczc |
| 59 | $C_2 \wr S_5$ | \( 1 - 20 T + 323 T^{2} - 3572 T^{3} + 33470 T^{4} - 273200 T^{5} + 33470 p T^{6} - 3572 p^{2} T^{7} + 323 p^{3} T^{8} - 20 p^{4} T^{9} + p^{5} T^{10} \) | 5.59.au_ml_afhk_bxni_apods |
| 61 | $C_2 \wr S_5$ | \( 1 - 7 T + 213 T^{2} - 1388 T^{3} + 21654 T^{4} - 116298 T^{5} + 21654 p T^{6} - 1388 p^{2} T^{7} + 213 p^{3} T^{8} - 7 p^{4} T^{9} + p^{5} T^{10} \) | 5.61.ah_if_acbk_bgaw_agqba |
| 67 | $C_2 \wr S_5$ | \( 1 - 11 T + 173 T^{2} - 1168 T^{3} + 18720 T^{4} - 127706 T^{5} + 18720 p T^{6} - 1168 p^{2} T^{7} + 173 p^{3} T^{8} - 11 p^{4} T^{9} + p^{5} T^{10} \) | 5.67.al_gr_absy_bbsa_ahgxu |
| 71 | $C_2 \wr S_5$ | \( 1 + 297 T^{2} - 250 T^{3} + 37704 T^{4} - 35628 T^{5} + 37704 p T^{6} - 250 p^{2} T^{7} + 297 p^{3} T^{8} + p^{5} T^{10} \) | 5.71.a_ll_ajq_cdue_acasi |
| 73 | $C_2 \wr S_5$ | \( 1 + 2 T + 107 T^{2} - 226 T^{3} + 10219 T^{4} - 14126 T^{5} + 10219 p T^{6} - 226 p^{2} T^{7} + 107 p^{3} T^{8} + 2 p^{4} T^{9} + p^{5} T^{10} \) | 5.73.c_ed_ais_pdb_auxi |
| 79 | $C_2 \wr S_5$ | \( 1 + 10 T + 235 T^{2} + 1778 T^{3} + 26189 T^{4} + 171648 T^{5} + 26189 p T^{6} + 1778 p^{2} T^{7} + 235 p^{3} T^{8} + 10 p^{4} T^{9} + p^{5} T^{10} \) | 5.79.k_jb_cqk_bmth_jtxw |
| 83 | $C_2 \wr S_5$ | \( 1 - 9 T + 238 T^{2} - 2373 T^{3} + 32325 T^{4} - 257468 T^{5} + 32325 p T^{6} - 2373 p^{2} T^{7} + 238 p^{3} T^{8} - 9 p^{4} T^{9} + p^{5} T^{10} \) | 5.83.aj_je_adnh_bvvh_aoqwq |
| 89 | $C_2 \wr S_5$ | \( 1 - 11 T + 208 T^{2} - 651 T^{3} + 11867 T^{4} + 25796 T^{5} + 11867 p T^{6} - 651 p^{2} T^{7} + 208 p^{3} T^{8} - 11 p^{4} T^{9} + p^{5} T^{10} \) | 5.89.al_ia_azb_rol_bmee |
| 97 | $C_2 \wr S_5$ | \( 1 + 24 T + 661 T^{2} + 9656 T^{3} + 145071 T^{4} + 1421078 T^{5} + 145071 p T^{6} + 9656 p^{2} T^{7} + 661 p^{3} T^{8} + 24 p^{4} T^{9} + p^{5} T^{10} \) | 5.97.y_zl_ohk_igpr_dcwew |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{10} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
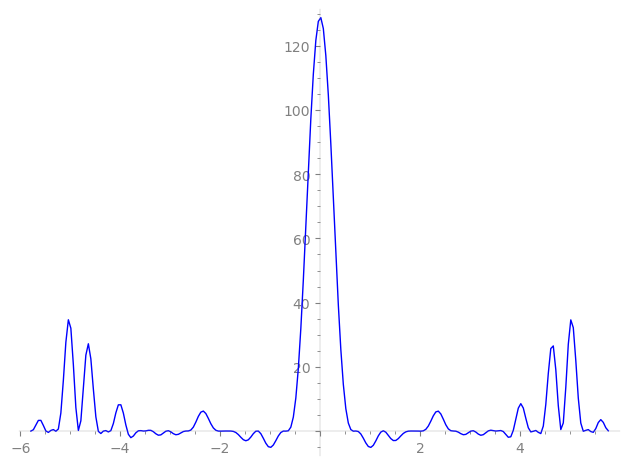
Imaginary part of the first few zeros on the critical line
−4.82306117258470983983769396397, −4.44000638772331223217902835533, −4.33510650050088141219741404672, −4.27129198131232680916419336918, −4.19280974010238579783681123168, −3.85852669921299059944081137130, −3.64636233429025254111284724142, −3.54146664457019283155142467354, −3.50218819903244596677163763805, −3.35739574947667428469716990303, −3.07921093383008961791197053670, −3.01670043200214155895134870513, −2.66972939379952804160396777606, −2.66553632479440019710558779633, −2.66243297144939474150742623989, −2.04762172263711257873965676005, −1.91102724909493266821558632682, −1.86188159359908724210784518014, −1.85891908831626149044349531826, −1.81271526754453131509414928210, −1.28012134695305910475548471707, −1.24010590968960861440206333119, −0.72925942782111856820736069992, −0.71096182288608834991158601065, −0.64720433930507915237343055810,
0.64720433930507915237343055810, 0.71096182288608834991158601065, 0.72925942782111856820736069992, 1.24010590968960861440206333119, 1.28012134695305910475548471707, 1.81271526754453131509414928210, 1.85891908831626149044349531826, 1.86188159359908724210784518014, 1.91102724909493266821558632682, 2.04762172263711257873965676005, 2.66243297144939474150742623989, 2.66553632479440019710558779633, 2.66972939379952804160396777606, 3.01670043200214155895134870513, 3.07921093383008961791197053670, 3.35739574947667428469716990303, 3.50218819903244596677163763805, 3.54146664457019283155142467354, 3.64636233429025254111284724142, 3.85852669921299059944081137130, 4.19280974010238579783681123168, 4.27129198131232680916419336918, 4.33510650050088141219741404672, 4.44000638772331223217902835533, 4.82306117258470983983769396397