↑

Properties

Label 4-2178e2-1.1-c1e2-0-27
Degree $4$
Conductor $4743684$
Sign $1$
Analytic cond. $302.461$
Root an. cond. $4.17030$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $2$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 2·2-s + 3·4-s − 5·5-s − 7-s − 4·8-s + 10·10-s + 4·13-s + 2·14-s + 5·16-s + 2·17-s + 4·19-s − 15·20-s − 10·23-s + 10·25-s − 8·26-s − 3·28-s − 3·29-s + 7·31-s − 6·32-s − 4·34-s + 5·35-s − 6·37-s − 8·38-s + 20·40-s + 18·41-s + 20·46-s − 14·47-s + ⋯
L(s)  = 1  − 1.41·2-s + 3/2·4-s − 2.23·5-s − 0.377·7-s − 1.41·8-s + 3.16·10-s + 1.10·13-s + 0.534·14-s + 5/4·16-s + 0.485·17-s + 0.917·19-s − 3.35·20-s − 2.08·23-s + 2·25-s − 1.56·26-s − 0.566·28-s − 0.557·29-s + 1.25·31-s − 1.06·32-s − 0.685·34-s + 0.845·35-s − 0.986·37-s − 1.29·38-s + 3.16·40-s + 2.81·41-s + 2.94·46-s − 2.04·47-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 4743684 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 4743684 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(4743684\)    =    \(2^{2} \cdot 3^{4} \cdot 11^{4}\)
Sign: $1$
Analytic conductor: \(302.461\)
Root analytic conductor: \(4.17030\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(2\)
Selberg data: \((4,\ 4743684,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(=\) \(0\)
\(L(\frac12)\) \(=\) \(0\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad2$C_1$ \( ( 1 + T )^{2} \)
3 \( 1 \)
11 \( 1 \)
good5$C_4$ \( 1 + p T + 3 p T^{2} + p^{2} T^{3} + p^{2} T^{4} \) 2.5.f_p
7$D_{4}$ \( 1 + T + 3 T^{2} + p T^{3} + p^{2} T^{4} \) 2.7.b_d
13$D_{4}$ \( 1 - 4 T + 10 T^{2} - 4 p T^{3} + p^{2} T^{4} \) 2.13.ae_k
17$D_{4}$ \( 1 - 2 T + 30 T^{2} - 2 p T^{3} + p^{2} T^{4} \) 2.17.ac_be
19$C_2$ \( ( 1 - 2 T + p T^{2} )^{2} \) 2.19.ae_bq
23$D_{4}$ \( 1 + 10 T + 66 T^{2} + 10 p T^{3} + p^{2} T^{4} \) 2.23.k_co
29$D_{4}$ \( 1 + 3 T + 59 T^{2} + 3 p T^{3} + p^{2} T^{4} \) 2.29.d_ch
31$D_{4}$ \( 1 - 7 T + 63 T^{2} - 7 p T^{3} + p^{2} T^{4} \) 2.31.ah_cl
37$D_{4}$ \( 1 + 6 T + 38 T^{2} + 6 p T^{3} + p^{2} T^{4} \) 2.37.g_bm
41$D_{4}$ \( 1 - 18 T + 158 T^{2} - 18 p T^{3} + p^{2} T^{4} \) 2.41.as_gc
43$C_2$ \( ( 1 + p T^{2} )^{2} \) 2.43.a_di
47$D_{4}$ \( 1 + 14 T + 138 T^{2} + 14 p T^{3} + p^{2} T^{4} \) 2.47.o_fi
53$D_{4}$ \( 1 + 21 T + 215 T^{2} + 21 p T^{3} + p^{2} T^{4} \) 2.53.v_ih
59$D_{4}$ \( 1 + 9 T + 77 T^{2} + 9 p T^{3} + p^{2} T^{4} \) 2.59.j_cz
61$D_{4}$ \( 1 - 10 T + 142 T^{2} - 10 p T^{3} + p^{2} T^{4} \) 2.61.ak_fm
67$D_{4}$ \( 1 + 4 T + 58 T^{2} + 4 p T^{3} + p^{2} T^{4} \) 2.67.e_cg
71$D_{4}$ \( 1 - 6 T + 146 T^{2} - 6 p T^{3} + p^{2} T^{4} \) 2.71.ag_fq
73$D_{4}$ \( 1 + 7 T + 157 T^{2} + 7 p T^{3} + p^{2} T^{4} \) 2.73.h_gb
79$D_{4}$ \( 1 + 21 T + 257 T^{2} + 21 p T^{3} + p^{2} T^{4} \) 2.79.v_jx
83$D_{4}$ \( 1 - 9 T + 35 T^{2} - 9 p T^{3} + p^{2} T^{4} \) 2.83.aj_bj
89$D_{4}$ \( 1 + 10 T + 78 T^{2} + 10 p T^{3} + p^{2} T^{4} \) 2.89.k_da
97$D_{4}$ \( 1 + 21 T + 293 T^{2} + 21 p T^{3} + p^{2} T^{4} \) 2.97.v_lh
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

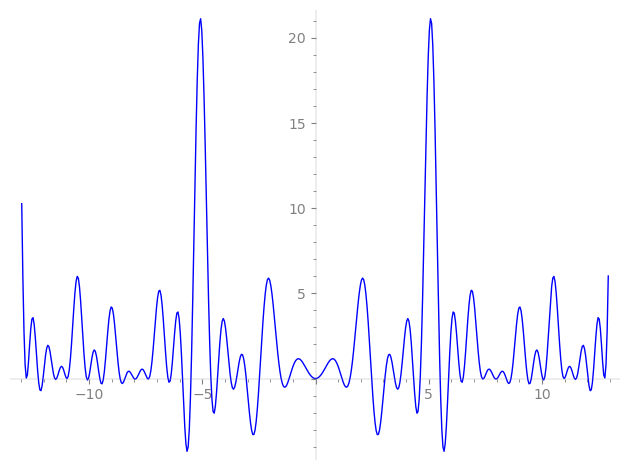
Imaginary part of the first few zeros on the critical line

−8.629439165609285898907644289429, −8.419985502611853216592282046190, −8.016527352112834482785588589697, −7.918534977369073433483616323985, −7.42631435575638246465860390033, −7.35981472977415451118346132051, −6.51556746888671985315295674546, −6.40068605228624602854775948730, −5.87343232190731310890494276227, −5.50129616621454727250192679238, −4.62142174877065404649797762229, −4.33129997194250338568940064008, −3.74933599973590598254477986059, −3.49139028484960511718272025294, −3.06155745138834253671807696552, −2.47878448233966675417859401854, −1.51965085135759145438759090131, −1.16663711169514261162866189356, 0, 0, 1.16663711169514261162866189356, 1.51965085135759145438759090131, 2.47878448233966675417859401854, 3.06155745138834253671807696552, 3.49139028484960511718272025294, 3.74933599973590598254477986059, 4.33129997194250338568940064008, 4.62142174877065404649797762229, 5.50129616621454727250192679238, 5.87343232190731310890494276227, 6.40068605228624602854775948730, 6.51556746888671985315295674546, 7.35981472977415451118346132051, 7.42631435575638246465860390033, 7.918534977369073433483616323985, 8.016527352112834482785588589697, 8.419985502611853216592282046190, 8.629439165609285898907644289429

Graph of the $Z$-function along the critical line