↑

Properties

Label 4-1053e2-1.1-c1e2-0-18
Degree $4$
Conductor $1108809$
Sign $1$
Analytic cond. $70.6986$
Root an. cond. $2.89969$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank $0$

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 4-s + 7·7-s + 2·13-s − 3·16-s + 19-s + 8·25-s − 7·28-s − 5·31-s + 7·37-s + 19·43-s + 25·49-s − 2·52-s − 14·61-s + 7·64-s − 11·67-s + 73-s − 76-s + 16·79-s + 14·91-s + 7·97-s − 8·100-s + 10·103-s − 23·109-s − 21·112-s + 8·121-s + 5·124-s + 127-s + ⋯
L(s)  = 1  − 1/2·4-s + 2.64·7-s + 0.554·13-s − 3/4·16-s + 0.229·19-s + 8/5·25-s − 1.32·28-s − 0.898·31-s + 1.15·37-s + 2.89·43-s + 25/7·49-s − 0.277·52-s − 1.79·61-s + 7/8·64-s − 1.34·67-s + 0.117·73-s − 0.114·76-s + 1.80·79-s + 1.46·91-s + 0.710·97-s − 4/5·100-s + 0.985·103-s − 2.20·109-s − 1.98·112-s + 8/11·121-s + 0.449·124-s + 0.0887·127-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1108809 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1108809 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(1108809\)    =    \(3^{8} \cdot 13^{2}\)
Sign: $1$
Analytic conductor: \(70.6986\)
Root analytic conductor: \(2.89969\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 1108809,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(2.949389133\)
\(L(\frac12)\) \(\approx\) \(2.949389133\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad3 \( 1 \)
13$C_1$ \( ( 1 - T )^{2} \)
good2$C_2^2$ \( 1 + T^{2} + p^{2} T^{4} \) 2.2.a_b
5$C_2^2$ \( 1 - 8 T^{2} + p^{2} T^{4} \) 2.5.a_ai
7$C_2$$\times$$C_2$ \( ( 1 - 5 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.7.ah_y
11$C_2^2$ \( 1 - 8 T^{2} + p^{2} T^{4} \) 2.11.a_ai
17$C_2^2$ \( 1 + T^{2} + p^{2} T^{4} \) 2.17.a_b
19$C_2$$\times$$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + T + p T^{2} ) \) 2.19.ab_bk
23$C_2^2$ \( 1 - 17 T^{2} + p^{2} T^{4} \) 2.23.a_ar
29$C_2^2$ \( 1 - 17 T^{2} + p^{2} T^{4} \) 2.29.a_ar
31$C_2$$\times$$C_2$ \( ( 1 - 5 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.31.f_m
37$C_2$$\times$$C_2$ \( ( 1 - 11 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) 2.37.ah_be
41$C_2^2$ \( 1 + 64 T^{2} + p^{2} T^{4} \) 2.41.a_cm
43$C_2$$\times$$C_2$ \( ( 1 - 11 T + p T^{2} )( 1 - 8 T + p T^{2} ) \) 2.43.at_gs
47$C_2^2$ \( 1 - 32 T^{2} + p^{2} T^{4} \) 2.47.a_abg
53$C_2$ \( ( 1 - 9 T + p T^{2} )( 1 + 9 T + p T^{2} ) \) 2.53.a_z
59$C_2^2$ \( 1 + 88 T^{2} + p^{2} T^{4} \) 2.59.a_dk
61$C_2$$\times$$C_2$ \( ( 1 + 4 T + p T^{2} )( 1 + 10 T + p T^{2} ) \) 2.61.o_gg
67$C_2$$\times$$C_2$ \( ( 1 - 2 T + p T^{2} )( 1 + 13 T + p T^{2} ) \) 2.67.l_ee
71$C_2^2$ \( 1 + 46 T^{2} + p^{2} T^{4} \) 2.71.a_bu
73$C_2$$\times$$C_2$ \( ( 1 - 14 T + p T^{2} )( 1 + 13 T + p T^{2} ) \) 2.73.ab_abk
79$C_2$$\times$$C_2$ \( ( 1 - 14 T + p T^{2} )( 1 - 2 T + p T^{2} ) \) 2.79.aq_he
83$C_2^2$ \( 1 + 148 T^{2} + p^{2} T^{4} \) 2.83.a_fs
89$C_2^2$ \( 1 - 8 T^{2} + p^{2} T^{4} \) 2.89.a_ai
97$C_2$$\times$$C_2$ \( ( 1 - 8 T + p T^{2} )( 1 + T + p T^{2} ) \) 2.97.ah_he
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

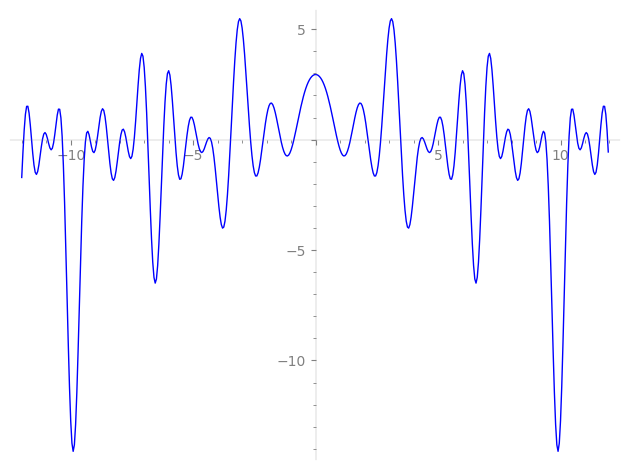
Imaginary part of the first few zeros on the critical line

−7.985090580364555816909935555633, −7.73255113962640828983385568681, −7.40898675704143229224136719922, −6.85601126037312811988469633481, −6.22352332095808095109214182636, −5.73929666698500247245024182477, −5.27342880744663435503755340410, −4.83524029416026843947618665230, −4.41423671973534029360550971540, −4.27725552030845210541887284628, −3.47177779696055329568185559602, −2.65832453194498384528279836396, −2.14023818286116106329815823247, −1.42360122444256523249385438297, −0.887310121126536044251794560117, 0.887310121126536044251794560117, 1.42360122444256523249385438297, 2.14023818286116106329815823247, 2.65832453194498384528279836396, 3.47177779696055329568185559602, 4.27725552030845210541887284628, 4.41423671973534029360550971540, 4.83524029416026843947618665230, 5.27342880744663435503755340410, 5.73929666698500247245024182477, 6.22352332095808095109214182636, 6.85601126037312811988469633481, 7.40898675704143229224136719922, 7.73255113962640828983385568681, 7.985090580364555816909935555633

Graph of the $Z$-function along the critical line