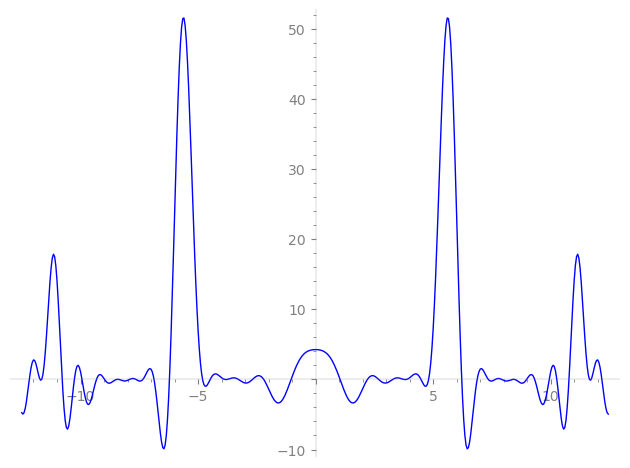
| L(s) = 1 | + 6·3-s − 6·5-s + 21·9-s + 11-s − 36·15-s − 2·23-s + 17·25-s + 54·27-s + 14·31-s + 6·33-s − 2·37-s − 126·45-s + 16·47-s − 10·49-s + 4·53-s − 6·55-s + 2·59-s + 10·67-s − 12·69-s − 6·71-s + 102·75-s + 108·81-s + 30·89-s + 84·93-s − 14·97-s + 21·99-s + 32·103-s + ⋯ |
| L(s) = 1 | + 3.46·3-s − 2.68·5-s + 7·9-s + 0.301·11-s − 9.29·15-s − 0.417·23-s + 17/5·25-s + 10.3·27-s + 2.51·31-s + 1.04·33-s − 0.328·37-s − 18.7·45-s + 2.33·47-s − 1.42·49-s + 0.549·53-s − 0.809·55-s + 0.260·59-s + 1.22·67-s − 1.44·69-s − 0.712·71-s + 11.7·75-s + 12·81-s + 3.17·89-s + 8.71·93-s − 1.42·97-s + 2.11·99-s + 3.15·103-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 340736 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 340736 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(4.245121724\) |
| \(L(\frac12)\) |
\(\approx\) |
\(4.245121724\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 11 | $C_1$ | \( 1 - T \) |
| good | 3 | $C_2$ | \( ( 1 - p T + p T^{2} )^{2} \) |
| 5 | $C_2$ | \( ( 1 + 3 T + p T^{2} )^{2} \) |
| 7 | $C_2$ | \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) |
| 13 | $C_2$ | \( ( 1 + p T^{2} )^{2} \) |
| 17 | $C_2$ | \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) |
| 19 | $C_2$ | \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) |
| 23 | $C_2$ | \( ( 1 + T + p T^{2} )^{2} \) |
| 29 | $C_2$ | \( ( 1 - 8 T + p T^{2} )( 1 + 8 T + p T^{2} ) \) |
| 31 | $C_2$ | \( ( 1 - 7 T + p T^{2} )^{2} \) |
| 37 | $C_2$ | \( ( 1 + T + p T^{2} )^{2} \) |
| 41 | $C_2$ | \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) |
| 43 | $C_2$ | \( ( 1 - 6 T + p T^{2} )( 1 + 6 T + p T^{2} ) \) |
| 47 | $C_2$ | \( ( 1 - 8 T + p T^{2} )^{2} \) |
| 53 | $C_2$ | \( ( 1 - 2 T + p T^{2} )^{2} \) |
| 59 | $C_2$ | \( ( 1 - T + p T^{2} )^{2} \) |
| 61 | $C_2$ | \( ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) |
| 67 | $C_2$ | \( ( 1 - 5 T + p T^{2} )^{2} \) |
| 71 | $C_2$ | \( ( 1 + 3 T + p T^{2} )^{2} \) |
| 73 | $C_2$ | \( ( 1 - 16 T + p T^{2} )( 1 + 16 T + p T^{2} ) \) |
| 79 | $C_2$ | \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) |
| 83 | $C_2$ | \( ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} ) \) |
| 89 | $C_2$ | \( ( 1 - 15 T + p T^{2} )^{2} \) |
| 97 | $C_2$ | \( ( 1 + 7 T + p T^{2} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.441695809340897861092685799301, −8.394339798874914668244789159293, −7.910918321149116453263180886740, −7.64755444346078841000957674432, −7.34464298147435526282636037125, −6.87292908671921502002689767413, −6.21679895699676402510107032244, −4.80898200433265196470127405375, −4.48090140750080174715782907716, −3.87401429056701171587588607766, −3.74300055016635814217609152843, −3.28681541538821572850087755824, −2.68030351930047444046477575602, −2.20819379597331931749827928065, −1.04001479698957226761907987971,
1.04001479698957226761907987971, 2.20819379597331931749827928065, 2.68030351930047444046477575602, 3.28681541538821572850087755824, 3.74300055016635814217609152843, 3.87401429056701171587588607766, 4.48090140750080174715782907716, 4.80898200433265196470127405375, 6.21679895699676402510107032244, 6.87292908671921502002689767413, 7.34464298147435526282636037125, 7.64755444346078841000957674432, 7.910918321149116453263180886740, 8.394339798874914668244789159293, 8.441695809340897861092685799301