| L(s) = 1 | − 2·2-s + 3·4-s − 6·8-s − 9-s + 9·16-s + 2·18-s − 2·23-s − 25-s + 2·29-s − 12·32-s − 3·36-s − 2·43-s + 4·46-s − 2·49-s + 2·50-s + 2·53-s − 4·58-s + 18·64-s − 2·67-s + 2·71-s + 6·72-s − 2·79-s + 81-s + 4·86-s − 6·92-s + 4·98-s − 3·100-s + ⋯ |
| L(s) = 1 | − 2·2-s + 3·4-s − 6·8-s − 9-s + 9·16-s + 2·18-s − 2·23-s − 25-s + 2·29-s − 12·32-s − 3·36-s − 2·43-s + 4·46-s − 2·49-s + 2·50-s + 2·53-s − 4·58-s + 18·64-s − 2·67-s + 2·71-s + 6·72-s − 2·79-s + 81-s + 4·86-s − 6·92-s + 4·98-s − 3·100-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(7^{4} \cdot 19^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(7^{4} \cdot 19^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(0.06006101219\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.06006101219\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 7 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 19 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| good | 2 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 3 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 5 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 11 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 13 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 17 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 23 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 29 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 31 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 37 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 41 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 43 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 47 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 53 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 59 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 61 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 67 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 71 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 73 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 79 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 83 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 89 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 97 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
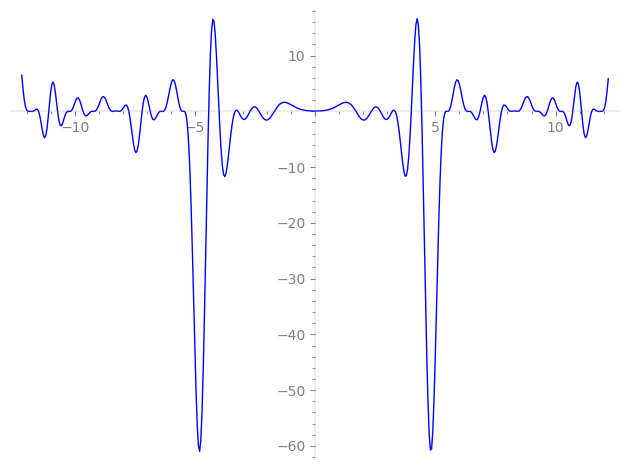
Imaginary part of the first few zeros on the critical line
−10.17226644292946765125862866461, −9.656034681280208466440361484716, −9.285612671148327135423610248964, −9.239053692940039465874360737458, −9.180058689512610881312014020254, −8.456438373398409426979478515721, −8.385138826224672845299114718856, −8.159577564624528159149562240696, −8.142770115043182775628926715441, −7.75107999141018477134556915583, −7.19808119128069739656818853077, −6.86187592916030067191584686767, −6.43424301154797598532413666283, −6.40277395728024042605463354872, −6.30950169152618461941082530168, −5.53890719816988880382030444731, −5.49083214680502202454568705016, −5.43296173482710314264454112292, −4.42935228777675251968558759391, −3.99891080945266620293898225975, −3.33065637603436017905043258494, −3.20872019042703496496577222133, −2.71044367256582579166473223063, −2.33705050726053221832002406374, −1.69683603271289636518353803388,
1.69683603271289636518353803388, 2.33705050726053221832002406374, 2.71044367256582579166473223063, 3.20872019042703496496577222133, 3.33065637603436017905043258494, 3.99891080945266620293898225975, 4.42935228777675251968558759391, 5.43296173482710314264454112292, 5.49083214680502202454568705016, 5.53890719816988880382030444731, 6.30950169152618461941082530168, 6.40277395728024042605463354872, 6.43424301154797598532413666283, 6.86187592916030067191584686767, 7.19808119128069739656818853077, 7.75107999141018477134556915583, 8.142770115043182775628926715441, 8.159577564624528159149562240696, 8.385138826224672845299114718856, 8.456438373398409426979478515721, 9.180058689512610881312014020254, 9.239053692940039465874360737458, 9.285612671148327135423610248964, 9.656034681280208466440361484716, 10.17226644292946765125862866461