↑

Properties

Label 4-351e2-1.1-c1e2-0-17
Degree $4$
Conductor $123201$
Sign $1$
Analytic cond. $7.85540$
Root an. cond. $1.67414$
Motivic weight $1$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

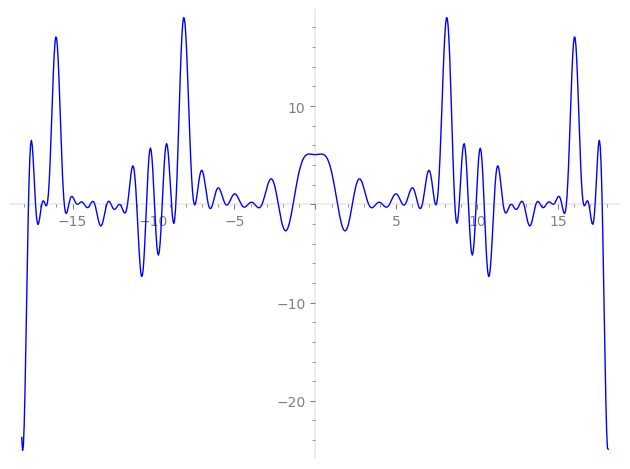
L(s)  = 1  + 3·2-s + 4·4-s + 3·8-s + 9·11-s − 5·13-s + 3·16-s + 6·17-s − 6·19-s + 27·22-s + 3·23-s − 2·25-s − 15·26-s − 6·29-s + 6·32-s + 18·34-s − 12·37-s − 18·38-s + 10·43-s + 36·44-s + 9·46-s − 7·49-s − 6·50-s − 20·52-s + 24·53-s − 18·58-s − 3·59-s − 10·61-s + ⋯
L(s)  = 1  + 2.12·2-s + 2·4-s + 1.06·8-s + 2.71·11-s − 1.38·13-s + 3/4·16-s + 1.45·17-s − 1.37·19-s + 5.75·22-s + 0.625·23-s − 2/5·25-s − 2.94·26-s − 1.11·29-s + 1.06·32-s + 3.08·34-s − 1.97·37-s − 2.91·38-s + 1.52·43-s + 5.42·44-s + 1.32·46-s − 49-s − 0.848·50-s − 2.77·52-s + 3.29·53-s − 2.36·58-s − 0.390·59-s − 1.28·61-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 123201 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 123201 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(123201\)    =    \(3^{6} \cdot 13^{2}\)
Sign: $1$
Analytic conductor: \(7.85540\)
Root analytic conductor: \(1.67414\)
Motivic weight: \(1\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 123201,\ (\ :1/2, 1/2),\ 1)\)

Particular Values

\(L(1)\) \(\approx\) \(5.058864021\)
\(L(\frac12)\) \(\approx\) \(5.058864021\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$Isogeny Class over $\mathbf{F}_p$
bad3 \( 1 \)
13$C_2$ \( 1 + 5 T + p T^{2} \)
good2$C_2^2$ \( 1 - 3 T + 5 T^{2} - 3 p T^{3} + p^{2} T^{4} \) 2.2.ad_f
5$C_2^2$ \( 1 + 2 T^{2} + p^{2} T^{4} \) 2.5.a_c
7$C_2^2$ \( 1 + p T^{2} + p^{2} T^{4} \) 2.7.a_h
11$C_2^2$ \( 1 - 9 T + 38 T^{2} - 9 p T^{3} + p^{2} T^{4} \) 2.11.aj_bm
17$C_2^2$ \( 1 - 6 T + 19 T^{2} - 6 p T^{3} + p^{2} T^{4} \) 2.17.ag_t
19$C_2$ \( ( 1 - T + p T^{2} )( 1 + 7 T + p T^{2} ) \) 2.19.g_bf
23$C_2^2$ \( 1 - 3 T - 14 T^{2} - 3 p T^{3} + p^{2} T^{4} \) 2.23.ad_ao
29$C_2^2$ \( 1 + 6 T + 7 T^{2} + 6 p T^{3} + p^{2} T^{4} \) 2.29.g_h
31$C_2^2$ \( 1 - 50 T^{2} + p^{2} T^{4} \) 2.31.a_aby
37$C_2$ \( ( 1 + T + p T^{2} )( 1 + 11 T + p T^{2} ) \) 2.37.m_dh
41$C_2^2$ \( 1 + p T^{2} + p^{2} T^{4} \) 2.41.a_bp
43$C_2^2$ \( 1 - 10 T + 57 T^{2} - 10 p T^{3} + p^{2} T^{4} \) 2.43.ak_cf
47$C_2^2$ \( 1 - 91 T^{2} + p^{2} T^{4} \) 2.47.a_adn
53$C_2$ \( ( 1 - 12 T + p T^{2} )^{2} \) 2.53.ay_jq
59$C_2^2$ \( 1 + 3 T + 62 T^{2} + 3 p T^{3} + p^{2} T^{4} \) 2.59.d_ck
61$C_2^2$ \( 1 + 10 T + 39 T^{2} + 10 p T^{3} + p^{2} T^{4} \) 2.61.k_bn
67$C_2$ \( ( 1 - 11 T + p T^{2} )( 1 + 5 T + p T^{2} ) \) 2.67.ag_db
71$C_2^2$ \( 1 + 6 T + 83 T^{2} + 6 p T^{3} + p^{2} T^{4} \) 2.71.g_df
73$C_2$ \( ( 1 - 17 T + p T^{2} )( 1 + 17 T + p T^{2} ) \) 2.73.a_afn
79$C_2$ \( ( 1 - 4 T + p T^{2} )^{2} \) 2.79.ai_gs
83$C_2^2$ \( 1 - 91 T^{2} + p^{2} T^{4} \) 2.83.a_adn
89$C_2^2$ \( 1 + 6 T + 101 T^{2} + 6 p T^{3} + p^{2} T^{4} \) 2.89.g_dx
97$C_2^2$ \( 1 + 15 T + 172 T^{2} + 15 p T^{3} + p^{2} T^{4} \) 2.97.p_gq
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−12.09678756008043903637374763031, −11.60876117752883010327366511031, −11.03929085083311150265487833390, −10.43450287917992193094796599668, −9.938986447567854229470602265735, −9.462445153213793659913022894046, −8.889901466523473173770970565234, −8.622579749543130120769543866343, −7.48596435643296082035869539211, −7.41838295389149176088128981064, −6.61152506784275796473559066203, −6.34727400554280995103918128230, −5.54930880361252748381352228643, −5.39306561661393449706957910324, −4.58091036402556046820590555862, −4.15096721305221661392689289843, −3.74515644327608918992984510229, −3.29764155144046298713531474638, −2.28728294708634059698859480543, −1.37551966031695442040981340406, 1.37551966031695442040981340406, 2.28728294708634059698859480543, 3.29764155144046298713531474638, 3.74515644327608918992984510229, 4.15096721305221661392689289843, 4.58091036402556046820590555862, 5.39306561661393449706957910324, 5.54930880361252748381352228643, 6.34727400554280995103918128230, 6.61152506784275796473559066203, 7.41838295389149176088128981064, 7.48596435643296082035869539211, 8.622579749543130120769543866343, 8.889901466523473173770970565234, 9.462445153213793659913022894046, 9.938986447567854229470602265735, 10.43450287917992193094796599668, 11.03929085083311150265487833390, 11.60876117752883010327366511031, 12.09678756008043903637374763031

Graph of the $Z$-function along the critical line