| L(s) = 1 | − 8·2-s + 16·4-s + 12·5-s + 176·7-s + 128·8-s − 96·10-s + 540·11-s + 446·13-s − 1.40e3·14-s − 1.02e3·16-s − 3.12e3·17-s − 3.18e3·19-s + 192·20-s − 4.32e3·22-s + 1.40e3·23-s + 5.61e3·25-s − 3.56e3·26-s + 2.81e3·28-s + 2.34e3·29-s + 776·31-s + 2.04e3·32-s + 2.49e4·34-s + 2.11e3·35-s + 7.05e3·37-s + 2.54e4·38-s + 1.53e3·40-s + 2.78e4·41-s + ⋯ |
| L(s) = 1 | − 1.41·2-s + 1/2·4-s + 0.214·5-s + 1.35·7-s + 0.707·8-s − 0.303·10-s + 1.34·11-s + 0.731·13-s − 1.91·14-s − 16-s − 2.61·17-s − 2.02·19-s + 0.107·20-s − 1.90·22-s + 0.553·23-s + 1.79·25-s − 1.03·26-s + 0.678·28-s + 0.516·29-s + 0.145·31-s + 0.353·32-s + 3.70·34-s + 0.291·35-s + 0.846·37-s + 2.86·38-s + 0.151·40-s + 2.58·41-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{16}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(6-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{16}\right)^{s/2} \, \Gamma_{\C}(s+5/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(3)\) |
\(\approx\) |
\(1.061340457\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.061340457\) |
| \(L(\frac{7}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 + p^{2} T + p^{4} T^{2} )^{2} \) |
| 3 | | \( 1 \) |
| good | 5 | $D_4\times C_2$ | \( 1 - 12 T - 5467 T^{2} + 7668 T^{3} + 21267696 T^{4} + 7668 p^{5} T^{5} - 5467 p^{10} T^{6} - 12 p^{15} T^{7} + p^{20} T^{8} \) |
| 7 | $D_4\times C_2$ | \( 1 - 176 T + 2686 T^{2} + 937024 T^{3} - 2764781 T^{4} + 937024 p^{5} T^{5} + 2686 p^{10} T^{6} - 176 p^{15} T^{7} + p^{20} T^{8} \) |
| 11 | $D_4\times C_2$ | \( 1 - 540 T - 18730 T^{2} + 6356880 T^{3} + 23404812699 T^{4} + 6356880 p^{5} T^{5} - 18730 p^{10} T^{6} - 540 p^{15} T^{7} + p^{20} T^{8} \) |
| 13 | $D_4\times C_2$ | \( 1 - 446 T - 593291 T^{2} - 1702382 p T^{3} + 2460812548 p^{2} T^{4} - 1702382 p^{6} T^{5} - 593291 p^{10} T^{6} - 446 p^{15} T^{7} + p^{20} T^{8} \) |
| 17 | $D_{4}$ | \( ( 1 + 1560 T + 3172687 T^{2} + 1560 p^{5} T^{3} + p^{10} T^{4} )^{2} \) |
| 19 | $D_{4}$ | \( ( 1 + 1592 T + 5183946 T^{2} + 1592 p^{5} T^{3} + p^{10} T^{4} )^{2} \) |
| 23 | $D_4\times C_2$ | \( 1 - 1404 T - 9890482 T^{2} + 61714224 p T^{3} + 163678536723 p^{2} T^{4} + 61714224 p^{6} T^{5} - 9890482 p^{10} T^{6} - 1404 p^{15} T^{7} + p^{20} T^{8} \) |
| 29 | $D_4\times C_2$ | \( 1 - 2340 T - 6176395 T^{2} + 68726509020 T^{3} - 397249093284576 T^{4} + 68726509020 p^{5} T^{5} - 6176395 p^{10} T^{6} - 2340 p^{15} T^{7} + p^{20} T^{8} \) |
| 31 | $D_4\times C_2$ | \( 1 - 776 T + 34207522 T^{2} + 70510190848 T^{3} + 292451205166339 T^{4} + 70510190848 p^{5} T^{5} + 34207522 p^{10} T^{6} - 776 p^{15} T^{7} + p^{20} T^{8} \) |
| 37 | $D_{4}$ | \( ( 1 - 3526 T + 28328583 T^{2} - 3526 p^{5} T^{3} + p^{10} T^{4} )^{2} \) |
| 41 | $D_4\times C_2$ | \( 1 - 27840 T + 353164190 T^{2} - 5294861982720 T^{3} + 74781984508050099 T^{4} - 5294861982720 p^{5} T^{5} + 353164190 p^{10} T^{6} - 27840 p^{15} T^{7} + p^{20} T^{8} \) |
| 43 | $D_4\times C_2$ | \( 1 + 23104 T + 162783958 T^{2} + 1778868729088 T^{3} + 37565229658980427 T^{4} + 1778868729088 p^{5} T^{5} + 162783958 p^{10} T^{6} + 23104 p^{15} T^{7} + p^{20} T^{8} \) |
| 47 | $D_4\times C_2$ | \( 1 - 38784 T + 722681810 T^{2} - 266393954304 p T^{3} + 96509278884675 p^{2} T^{4} - 266393954304 p^{6} T^{5} + 722681810 p^{10} T^{6} - 38784 p^{15} T^{7} + p^{20} T^{8} \) |
| 53 | $D_{4}$ | \( ( 1 + 45672 T + 1133302570 T^{2} + 45672 p^{5} T^{3} + p^{10} T^{4} )^{2} \) |
| 59 | $D_4\times C_2$ | \( 1 - 2160 T - 480096598 T^{2} + 2041386624000 T^{3} - 279457915500264597 T^{4} + 2041386624000 p^{5} T^{5} - 480096598 p^{10} T^{6} - 2160 p^{15} T^{7} + p^{20} T^{8} \) |
| 61 | $D_4\times C_2$ | \( 1 + 8974 T - 1161991067 T^{2} - 4008406340666 T^{3} + 762504739996615972 T^{4} - 4008406340666 p^{5} T^{5} - 1161991067 p^{10} T^{6} + 8974 p^{15} T^{7} + p^{20} T^{8} \) |
| 67 | $D_4\times C_2$ | \( 1 + 71656 T + 2232546838 T^{2} + 14459126310304 T^{3} - 333356298691963397 T^{4} + 14459126310304 p^{5} T^{5} + 2232546838 p^{10} T^{6} + 71656 p^{15} T^{7} + p^{20} T^{8} \) |
| 71 | $D_{4}$ | \( ( 1 + 348 p T + 3665651218 T^{2} + 348 p^{6} T^{3} + p^{10} T^{4} )^{2} \) |
| 73 | $D_{4}$ | \( ( 1 - 60322 T + 3938822259 T^{2} - 60322 p^{5} T^{3} + p^{10} T^{4} )^{2} \) |
| 79 | $D_4\times C_2$ | \( 1 + 74392 T - 1070611682 T^{2} + 33526134622816 T^{3} + 17125908368079844579 T^{4} + 33526134622816 p^{5} T^{5} - 1070611682 p^{10} T^{6} + 74392 p^{15} T^{7} + p^{20} T^{8} \) |
| 83 | $D_4\times C_2$ | \( 1 - 29496 T - 3514362022 T^{2} + 103050329995008 T^{3} + 279691486379071707 T^{4} + 103050329995008 p^{5} T^{5} - 3514362022 p^{10} T^{6} - 29496 p^{15} T^{7} + p^{20} T^{8} \) |
| 89 | $D_{4}$ | \( ( 1 - 110976 T + 7596045367 T^{2} - 110976 p^{5} T^{3} + p^{10} T^{4} )^{2} \) |
| 97 | $D_4\times C_2$ | \( 1 - 5564 T - 16734873974 T^{2} + 2274832742416 T^{3} + \)\(20\!\cdots\!79\)\( T^{4} + 2274832742416 p^{5} T^{5} - 16734873974 p^{10} T^{6} - 5564 p^{15} T^{7} + p^{20} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
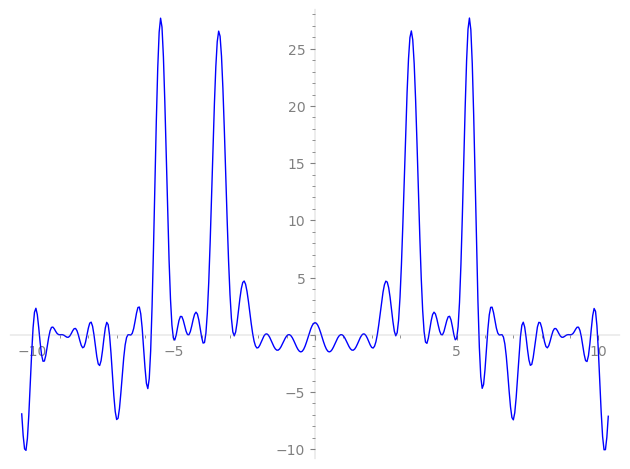
Imaginary part of the first few zeros on the critical line
−8.627087492876320545111044097511, −8.355614519691513043167325834377, −8.047767766372369971873310350050, −7.80300079358844894027158541677, −7.43625417667988921440937229007, −7.25449739041886831933076644047, −6.60337943698596226689246741759, −6.55381659367635129417598449078, −6.48443882134235017550026311290, −6.08365986592703037325240389449, −5.78223082267176963693846584019, −5.01969631826354111294753574337, −4.89916827673981769096616311167, −4.49785597365734948470280559618, −4.45132089994428802458688261808, −4.01806381857974807478117688819, −3.85825622253914635167211341249, −2.88056401868971062798928724182, −2.82738749490920860192237303641, −2.19569293810722560008865456737, −1.77358715059821654217282516560, −1.65905289548747462541588511978, −0.952205901572863795266846906436, −0.894167360997641740206481567512, −0.22073044085337699853641571382,
0.22073044085337699853641571382, 0.894167360997641740206481567512, 0.952205901572863795266846906436, 1.65905289548747462541588511978, 1.77358715059821654217282516560, 2.19569293810722560008865456737, 2.82738749490920860192237303641, 2.88056401868971062798928724182, 3.85825622253914635167211341249, 4.01806381857974807478117688819, 4.45132089994428802458688261808, 4.49785597365734948470280559618, 4.89916827673981769096616311167, 5.01969631826354111294753574337, 5.78223082267176963693846584019, 6.08365986592703037325240389449, 6.48443882134235017550026311290, 6.55381659367635129417598449078, 6.60337943698596226689246741759, 7.25449739041886831933076644047, 7.43625417667988921440937229007, 7.80300079358844894027158541677, 8.047767766372369971873310350050, 8.355614519691513043167325834377, 8.627087492876320545111044097511