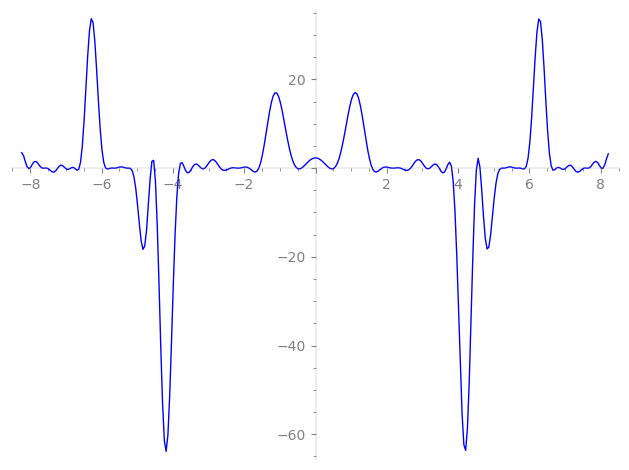
| L(s) = 1 | + 5·4-s − 2·9-s − 16·11-s + 12·16-s + 4·19-s − 12·29-s − 24·31-s − 10·36-s − 20·41-s − 80·44-s + 18·49-s + 32·59-s − 4·61-s + 15·64-s − 8·71-s + 20·76-s + 36·79-s + 3·81-s + 4·89-s + 32·99-s − 12·101-s + 4·109-s − 60·116-s + 116·121-s − 120·124-s + 127-s + 131-s + ⋯ |
| L(s) = 1 | + 5/2·4-s − 2/3·9-s − 4.82·11-s + 3·16-s + 0.917·19-s − 2.22·29-s − 4.31·31-s − 5/3·36-s − 3.12·41-s − 12.0·44-s + 18/7·49-s + 4.16·59-s − 0.512·61-s + 15/8·64-s − 0.949·71-s + 2.29·76-s + 4.05·79-s + 1/3·81-s + 0.423·89-s + 3.21·99-s − 1.19·101-s + 0.383·109-s − 5.57·116-s + 10.5·121-s − 10.7·124-s + 0.0887·127-s + 0.0873·131-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 5^{8} \cdot 19^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 5^{8} \cdot 19^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(2.313262471\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.313262471\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 3 | $C_2$ | \( ( 1 + T^{2} )^{2} \) | |
| 5 | | \( 1 \) | |
| 19 | $C_1$ | \( ( 1 - T )^{4} \) | |
| good | 2 | $D_4\times C_2$ | \( 1 - 5 T^{2} + 13 T^{4} - 5 p^{2} T^{6} + p^{4} T^{8} \) | 4.2.a_af_a_n |
| 7 | $C_2^2$ | \( ( 1 - 9 T^{2} + p^{2} T^{4} )^{2} \) | 4.7.a_as_a_gx |
| 11 | $C_2$ | \( ( 1 + 4 T + p T^{2} )^{4} \) | 4.11.q_fk_bee_epa |
| 13 | $D_4\times C_2$ | \( 1 - 4 T^{2} + 22 T^{4} - 4 p^{2} T^{6} + p^{4} T^{8} \) | 4.13.a_ae_a_w |
| 17 | $D_4\times C_2$ | \( 1 - 56 T^{2} + 1342 T^{4} - 56 p^{2} T^{6} + p^{4} T^{8} \) | 4.17.a_ace_a_bzq |
| 23 | $D_4\times C_2$ | \( 1 - 80 T^{2} + 2638 T^{4} - 80 p^{2} T^{6} + p^{4} T^{8} \) | 4.23.a_adc_a_dxm |
| 29 | $D_{4}$ | \( ( 1 + 6 T + 47 T^{2} + 6 p T^{3} + p^{2} T^{4} )^{2} \) | 4.29.m_fa_bjc_ivz |
| 31 | $D_{4}$ | \( ( 1 + 12 T + 78 T^{2} + 12 p T^{3} + p^{2} T^{4} )^{2} \) | 4.31.y_lo_dwq_zbi |
| 37 | $D_4\times C_2$ | \( 1 - 88 T^{2} + 4174 T^{4} - 88 p^{2} T^{6} + p^{4} T^{8} \) | 4.37.a_adk_a_geo |
| 41 | $C_2$ | \( ( 1 + 5 T + p T^{2} )^{4} \) | 4.41.u_mc_ejw_bibb |
| 43 | $C_2^2$ | \( ( 1 - 70 T^{2} + p^{2} T^{4} )^{2} \) | 4.43.a_afk_a_mss |
| 47 | $D_4\times C_2$ | \( 1 - 116 T^{2} + 6502 T^{4} - 116 p^{2} T^{6} + p^{4} T^{8} \) | 4.47.a_aem_a_jqc |
| 53 | $C_2^2$ | \( ( 1 - 81 T^{2} + p^{2} T^{4} )^{2} \) | 4.53.a_agg_a_sal |
| 59 | $D_{4}$ | \( ( 1 - 16 T + 137 T^{2} - 16 p T^{3} + p^{2} T^{4} )^{2} \) | 4.59.abg_uk_ajhg_detn |
| 61 | $D_{4}$ | \( ( 1 + 2 T + 43 T^{2} + 2 p T^{3} + p^{2} T^{4} )^{2} \) | 4.61.e_dm_qa_omd |
| 67 | $D_4\times C_2$ | \( 1 - 100 T^{2} + 10198 T^{4} - 100 p^{2} T^{6} + p^{4} T^{8} \) | 4.67.a_adw_a_pcg |
| 71 | $D_{4}$ | \( ( 1 + 4 T + 21 T^{2} + 4 p T^{3} + p^{2} T^{4} )^{2} \) | 4.71.i_cg_bci_syd |
| 73 | $D_4\times C_2$ | \( 1 - 250 T^{2} + 26203 T^{4} - 250 p^{2} T^{6} + p^{4} T^{8} \) | 4.73.a_ajq_a_bmtv |
| 79 | $D_{4}$ | \( ( 1 - 18 T + 194 T^{2} - 18 p T^{3} + p^{2} T^{4} )^{2} \) | 4.79.abk_bbk_aooa_ftwo |
| 83 | $D_4\times C_2$ | \( 1 - 164 T^{2} + 19222 T^{4} - 164 p^{2} T^{6} + p^{4} T^{8} \) | 4.83.a_agi_a_bcli |
| 89 | $D_{4}$ | \( ( 1 - 2 T + 99 T^{2} - 2 p T^{3} + p^{2} T^{4} )^{2} \) | 4.89.ae_hu_abcy_bmzr |
| 97 | $D_4\times C_2$ | \( 1 - 248 T^{2} + 29694 T^{4} - 248 p^{2} T^{6} + p^{4} T^{8} \) | 4.97.a_ajo_a_bryc |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.86651164417588873683717278384, −6.75607299530934056354079478074, −6.62694170130509033553134261255, −5.88420346710924251514826918127, −5.74832453796289410688024100113, −5.65670472493239329103341032846, −5.61509771488877472224313916475, −5.29152918455228038983265075880, −5.26532051184216963481459456202, −5.21324918922325643592157226714, −4.61311350784467770169161754741, −4.51454906045621808413549782053, −3.82045091169646273098333367898, −3.67232117945070526315595066969, −3.46772875231093882600242374618, −3.20519613158112948527303564123, −3.10369145586348187922038542723, −2.66696231278990812457603910566, −2.38200944548796501452422769612, −2.18742098784607666408074281651, −2.14578158825900728380585635354, −1.86413328042835971710134406324, −1.59038933078767992311029568140, −0.52101797173706123406503859616, −0.39610447143725474632307808322,
0.39610447143725474632307808322, 0.52101797173706123406503859616, 1.59038933078767992311029568140, 1.86413328042835971710134406324, 2.14578158825900728380585635354, 2.18742098784607666408074281651, 2.38200944548796501452422769612, 2.66696231278990812457603910566, 3.10369145586348187922038542723, 3.20519613158112948527303564123, 3.46772875231093882600242374618, 3.67232117945070526315595066969, 3.82045091169646273098333367898, 4.51454906045621808413549782053, 4.61311350784467770169161754741, 5.21324918922325643592157226714, 5.26532051184216963481459456202, 5.29152918455228038983265075880, 5.61509771488877472224313916475, 5.65670472493239329103341032846, 5.74832453796289410688024100113, 5.88420346710924251514826918127, 6.62694170130509033553134261255, 6.75607299530934056354079478074, 6.86651164417588873683717278384