| L(s) = 1 | + 2-s + 4-s − 2·5-s + 7-s + 8-s − 2·10-s + 6·11-s + 3·13-s + 14-s + 16-s + 17-s + 7·19-s − 2·20-s + 6·22-s − 3·23-s − 25-s + 3·26-s + 28-s − 2·29-s + 2·31-s + 32-s + 34-s − 2·35-s − 5·37-s + 7·38-s − 2·40-s + 9·41-s + ⋯ |
| L(s) = 1 | + 0.707·2-s + 1/2·4-s − 0.894·5-s + 0.377·7-s + 0.353·8-s − 0.632·10-s + 1.80·11-s + 0.832·13-s + 0.267·14-s + 1/4·16-s + 0.242·17-s + 1.60·19-s − 0.447·20-s + 1.27·22-s − 0.625·23-s − 1/5·25-s + 0.588·26-s + 0.188·28-s − 0.371·29-s + 0.359·31-s + 0.176·32-s + 0.171·34-s − 0.338·35-s − 0.821·37-s + 1.13·38-s − 0.316·40-s + 1.40·41-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 384678 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 384678 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 - T \) | |
| 3 | \( 1 \) | |
| 7 | \( 1 - T \) | |
| 43 | \( 1 - T \) | |
| 71 | \( 1 - T \) | |
| good | 5 | \( 1 + 2 T + p T^{2} \) | 1.5.c |
| 11 | \( 1 - 6 T + p T^{2} \) | 1.11.ag |
| 13 | \( 1 - 3 T + p T^{2} \) | 1.13.ad |
| 17 | \( 1 - T + p T^{2} \) | 1.17.ab |
| 19 | \( 1 - 7 T + p T^{2} \) | 1.19.ah |
| 23 | \( 1 + 3 T + p T^{2} \) | 1.23.d |
| 29 | \( 1 + 2 T + p T^{2} \) | 1.29.c |
| 31 | \( 1 - 2 T + p T^{2} \) | 1.31.ac |
| 37 | \( 1 + 5 T + p T^{2} \) | 1.37.f |
| 41 | \( 1 - 9 T + p T^{2} \) | 1.41.aj |
| 47 | \( 1 + 12 T + p T^{2} \) | 1.47.m |
| 53 | \( 1 - 2 T + p T^{2} \) | 1.53.ac |
| 59 | \( 1 - 4 T + p T^{2} \) | 1.59.ae |
| 61 | \( 1 + 6 T + p T^{2} \) | 1.61.g |
| 67 | \( 1 + 8 T + p T^{2} \) | 1.67.i |
| 73 | \( 1 + 10 T + p T^{2} \) | 1.73.k |
| 79 | \( 1 - 9 T + p T^{2} \) | 1.79.aj |
| 83 | \( 1 - 12 T + p T^{2} \) | 1.83.am |
| 89 | \( 1 + 13 T + p T^{2} \) | 1.89.n |
| 97 | \( 1 + 12 T + p T^{2} \) | 1.97.m |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
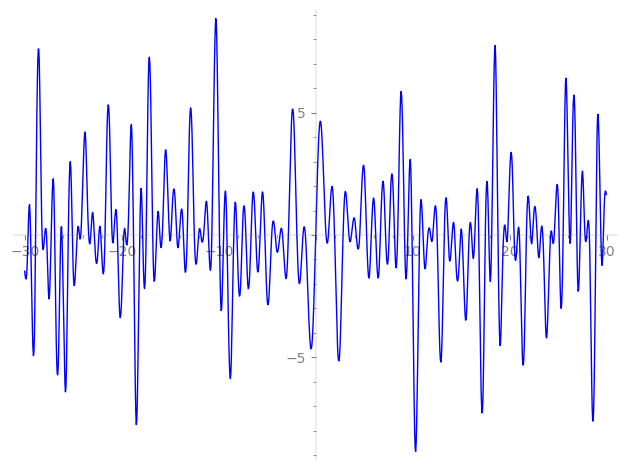
Imaginary part of the first few zeros on the critical line
−12.51523567878017, −12.07908386600918, −11.83108635432265, −11.54899034429968, −11.05869534216453, −10.70517008890514, −9.928896469655176, −9.494157027185138, −9.151862597178882, −8.448585438465351, −8.121108761603392, −7.571811729580651, −7.201405450991060, −6.664125343792507, −6.185138555879781, −5.729471547047896, −5.246301876556544, −4.536584471402620, −4.180075921582136, −3.686918530069052, −3.419728242861041, −2.816805447384747, −1.940486806173969, −1.310487222352136, −1.062494160781820, 0,
1.062494160781820, 1.310487222352136, 1.940486806173969, 2.816805447384747, 3.419728242861041, 3.686918530069052, 4.180075921582136, 4.536584471402620, 5.246301876556544, 5.729471547047896, 6.185138555879781, 6.664125343792507, 7.201405450991060, 7.571811729580651, 8.121108761603392, 8.448585438465351, 9.151862597178882, 9.494157027185138, 9.928896469655176, 10.70517008890514, 11.05869534216453, 11.54899034429968, 11.83108635432265, 12.07908386600918, 12.51523567878017