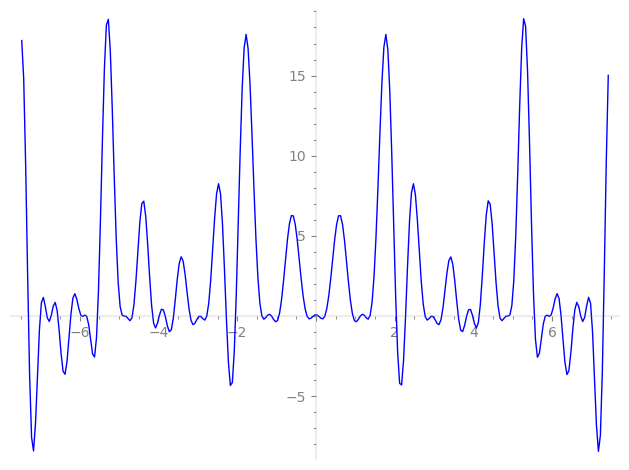
| L(s) = 1 | − 16·4-s − 80·7-s + 172·13-s + 192·16-s + 224·19-s + 1.28e3·28-s + 3.38e3·31-s − 200·37-s + 1.13e3·43-s − 5.60e3·49-s − 2.75e3·52-s − 808·61-s − 2.04e3·64-s − 1.20e3·67-s − 1.12e4·73-s − 3.58e3·76-s − 4.70e3·79-s − 1.37e4·91-s − 1.17e4·97-s − 2.45e4·103-s − 2.69e4·109-s − 1.53e4·112-s + 4.46e4·121-s − 5.40e4·124-s + 127-s + 131-s − 1.79e4·133-s + ⋯ |
| L(s) = 1 | − 4-s − 1.63·7-s + 1.01·13-s + 3/4·16-s + 0.620·19-s + 1.63·28-s + 3.51·31-s − 0.146·37-s + 0.612·43-s − 2.33·49-s − 1.01·52-s − 0.217·61-s − 1/2·64-s − 0.269·67-s − 2.10·73-s − 0.620·76-s − 0.754·79-s − 1.66·91-s − 1.25·97-s − 2.31·103-s − 2.26·109-s − 1.22·112-s + 3.04·121-s − 3.51·124-s + 6.20e−5·127-s + 5.82e−5·131-s − 1.01·133-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{12} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(5-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{12} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s+2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{5}{2})\) |
\(\approx\) |
\(0.08960281497\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.08960281497\) |
| \(L(3)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 + p^{3} T^{2} )^{2} \) |
| 3 | | \( 1 \) |
| 5 | | \( 1 \) |
| good | 7 | $C_2$ | \( ( 1 + 20 T + p^{4} T^{2} )^{4} \) |
| 11 | $D_4\times C_2$ | \( 1 - 44650 T^{2} + 900879387 T^{4} - 44650 p^{8} T^{6} + p^{16} T^{8} \) |
| 13 | $D_{4}$ | \( ( 1 - 86 T + 49971 T^{2} - 86 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 17 | $D_4\times C_2$ | \( 1 - 151690 T^{2} + 19677734907 T^{4} - 151690 p^{8} T^{6} + p^{16} T^{8} \) |
| 19 | $D_{4}$ | \( ( 1 - 112 T + 227778 T^{2} - 112 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 23 | $D_4\times C_2$ | \( 1 - 837898 T^{2} + 329631179163 T^{4} - 837898 p^{8} T^{6} + p^{16} T^{8} \) |
| 29 | $D_4\times C_2$ | \( 1 - 960058 T^{2} + 438385562763 T^{4} - 960058 p^{8} T^{6} + p^{16} T^{8} \) |
| 31 | $D_{4}$ | \( ( 1 - 1690 T + 2120067 T^{2} - 1690 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 37 | $D_{4}$ | \( ( 1 + 100 T + 150822 T^{2} + 100 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 41 | $D_4\times C_2$ | \( 1 - 10178908 T^{2} + 41862356252358 T^{4} - 10178908 p^{8} T^{6} + p^{16} T^{8} \) |
| 43 | $D_{4}$ | \( ( 1 - 566 T + 833691 T^{2} - 566 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 47 | $D_4\times C_2$ | \( 1 - 17403418 T^{2} + 123121255420203 T^{4} - 17403418 p^{8} T^{6} + p^{16} T^{8} \) |
| 53 | $D_4\times C_2$ | \( 1 - 23246428 T^{2} + 253968256288518 T^{4} - 23246428 p^{8} T^{6} + p^{16} T^{8} \) |
| 59 | $D_4\times C_2$ | \( 1 - 46182940 T^{2} + 825741441553542 T^{4} - 46182940 p^{8} T^{6} + p^{16} T^{8} \) |
| 61 | $D_{4}$ | \( ( 1 + 404 T + 17328486 T^{2} + 404 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 67 | $C_2$ | \( ( 1 + 302 T + p^{4} T^{2} )^{4} \) |
| 71 | $D_4\times C_2$ | \( 1 - 84014788 T^{2} + 3052505136298758 T^{4} - 84014788 p^{8} T^{6} + p^{16} T^{8} \) |
| 73 | $D_{4}$ | \( ( 1 + 5608 T + 64622898 T^{2} + 5608 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 79 | $D_{4}$ | \( ( 1 + 2354 T + 17284491 T^{2} + 2354 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| 83 | $D_4\times C_2$ | \( 1 - 105825628 T^{2} + 5551353165612678 T^{4} - 105825628 p^{8} T^{6} + p^{16} T^{8} \) |
| 89 | $D_4\times C_2$ | \( 1 - 204814660 T^{2} + 18017961082477062 T^{4} - 204814660 p^{8} T^{6} + p^{16} T^{8} \) |
| 97 | $D_{4}$ | \( ( 1 + 5884 T + 136429926 T^{2} + 5884 p^{4} T^{3} + p^{8} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.22810771774692787632940859587, −5.95589929335075574829271097358, −5.90783976597844968691379021948, −5.82622471520749115198193528561, −5.54754457833900882841322677310, −4.89567456639696179205835942798, −4.87843382353742638410887212512, −4.83283312863083630686655926595, −4.66404867312323227190041203304, −4.14857319652057775252836417116, −3.98174325956324071228528096638, −3.82806107269708290899030053205, −3.61656713397593383051340730222, −3.19573328960721536646951214254, −2.96011581161248698234140565457, −2.93680883189456643958916576170, −2.77297264796011869082379236712, −2.27693672533291116329516814668, −2.04092251013588735043146030219, −1.37239327135827776962786047507, −1.24756970523550051829068449817, −1.12638282309505174331952133554, −0.939302636562857865075835167831, −0.22570845478582192693459520804, −0.06892705514984856887477074880,
0.06892705514984856887477074880, 0.22570845478582192693459520804, 0.939302636562857865075835167831, 1.12638282309505174331952133554, 1.24756970523550051829068449817, 1.37239327135827776962786047507, 2.04092251013588735043146030219, 2.27693672533291116329516814668, 2.77297264796011869082379236712, 2.93680883189456643958916576170, 2.96011581161248698234140565457, 3.19573328960721536646951214254, 3.61656713397593383051340730222, 3.82806107269708290899030053205, 3.98174325956324071228528096638, 4.14857319652057775252836417116, 4.66404867312323227190041203304, 4.83283312863083630686655926595, 4.87843382353742638410887212512, 4.89567456639696179205835942798, 5.54754457833900882841322677310, 5.82622471520749115198193528561, 5.90783976597844968691379021948, 5.95589929335075574829271097358, 6.22810771774692787632940859587