| L(s) = 1 | + 8·5-s + 8·13-s − 56·17-s − 60·25-s + 56·29-s + 104·37-s + 40·41-s − 14·49-s − 40·53-s − 24·61-s + 64·65-s + 232·73-s − 448·85-s − 152·89-s − 88·97-s − 152·101-s − 280·109-s + 248·113-s + 164·121-s − 840·125-s + 127-s + 131-s + 137-s + 139-s + 448·145-s + 149-s + 151-s + ⋯ |
| L(s) = 1 | + 8/5·5-s + 8/13·13-s − 3.29·17-s − 2.39·25-s + 1.93·29-s + 2.81·37-s + 0.975·41-s − 2/7·49-s − 0.754·53-s − 0.393·61-s + 0.984·65-s + 3.17·73-s − 5.27·85-s − 1.70·89-s − 0.907·97-s − 1.50·101-s − 2.56·109-s + 2.19·113-s + 1.35·121-s − 6.71·125-s + 0.00787·127-s + 0.00763·131-s + 0.00729·137-s + 0.00719·139-s + 3.08·145-s + 0.00671·149-s + 0.00662·151-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{8} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(3-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{8} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s+1)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{3}{2})\) |
\(\approx\) |
\(4.885270672\) |
| \(L(\frac12)\) |
\(\approx\) |
\(4.885270672\) |
| \(L(2)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | | \( 1 \) |
| 7 | $C_2$ | \( ( 1 + p T^{2} )^{2} \) |
| good | 5 | $C_2$ | \( ( 1 - 2 T + p^{2} T^{2} )^{4} \) |
| 11 | $D_4\times C_2$ | \( 1 - 164 T^{2} + 14502 T^{4} - 164 p^{4} T^{6} + p^{8} T^{8} \) |
| 13 | $D_{4}$ | \( ( 1 - 4 T + 6 T^{2} - 4 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 17 | $D_{4}$ | \( ( 1 + 28 T + 438 T^{2} + 28 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 19 | $D_4\times C_2$ | \( 1 - 452 T^{2} + 225702 T^{4} - 452 p^{4} T^{6} + p^{8} T^{8} \) |
| 23 | $D_4\times C_2$ | \( 1 - 1028 T^{2} + 630342 T^{4} - 1028 p^{4} T^{6} + p^{8} T^{8} \) |
| 29 | $D_{4}$ | \( ( 1 - 28 T + 534 T^{2} - 28 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 31 | $C_2^2$ | \( ( 1 - 1154 T^{2} + p^{4} T^{4} )^{2} \) |
| 37 | $D_{4}$ | \( ( 1 - 52 T + 2070 T^{2} - 52 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 41 | $D_{4}$ | \( ( 1 - 20 T + 3126 T^{2} - 20 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 43 | $D_4\times C_2$ | \( 1 - 4964 T^{2} + 11621670 T^{4} - 4964 p^{4} T^{6} + p^{8} T^{8} \) |
| 47 | $D_4\times C_2$ | \( 1 + 764 T^{2} - 2481018 T^{4} + 764 p^{4} T^{6} + p^{8} T^{8} \) |
| 53 | $D_{4}$ | \( ( 1 + 20 T + 4374 T^{2} + 20 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 59 | $D_4\times C_2$ | \( 1 - 12164 T^{2} + 60451302 T^{4} - 12164 p^{4} T^{6} + p^{8} T^{8} \) |
| 61 | $D_{4}$ | \( ( 1 + 12 T + 7142 T^{2} + 12 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - 122 T + p^{2} T^{2} )^{2}( 1 + 122 T + p^{2} T^{2} )^{2} \) |
| 71 | $D_4\times C_2$ | \( 1 - 8324 T^{2} + 58662342 T^{4} - 8324 p^{4} T^{6} + p^{8} T^{8} \) |
| 73 | $D_{4}$ | \( ( 1 - 116 T + 12678 T^{2} - 116 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 79 | $C_2^2$ | \( ( 1 - 3074 T^{2} + p^{4} T^{4} )^{2} \) |
| 83 | $D_4\times C_2$ | \( 1 - 12356 T^{2} + 120698022 T^{4} - 12356 p^{4} T^{6} + p^{8} T^{8} \) |
| 89 | $D_{4}$ | \( ( 1 + 76 T + 14262 T^{2} + 76 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 97 | $D_{4}$ | \( ( 1 + 44 T + 13926 T^{2} + 44 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
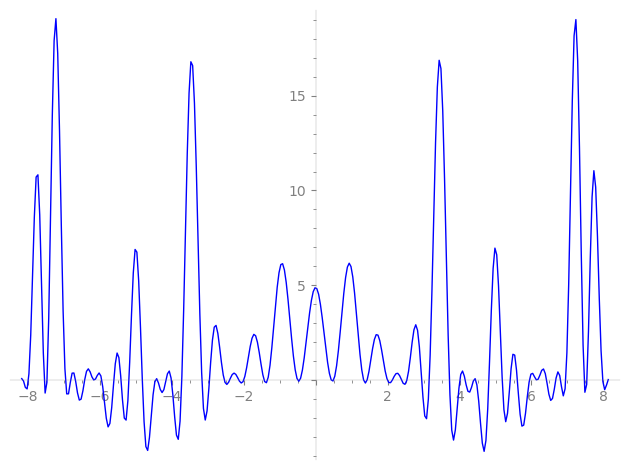
Imaginary part of the first few zeros on the critical line
−6.80543419223956823452040612074, −6.67440396070481376157460128941, −6.41691801419106463507159133991, −6.16957828395956178837673688583, −6.13541030575846247905842588754, −5.94373998749367109128577814168, −5.60565149586405895933027653742, −5.40791582005776150874754034297, −5.18711442836667646978261745305, −4.81556619777009654978729339033, −4.45204434341413563628072675829, −4.39528980206370327857375512028, −4.15525070154184011536883265379, −4.00953531069221543936457938232, −3.71918597690148423338195003855, −3.15863881630859248015302078944, −2.94965216852766916943593589809, −2.53859636580750126562302320329, −2.38699024214473629990325373520, −2.13558342819319987179677717980, −1.99467673071924519083284052964, −1.43252734112867369444821905008, −1.33348729079263205789684051862, −0.50228470896749233309757075532, −0.43329938221608958799330737254,
0.43329938221608958799330737254, 0.50228470896749233309757075532, 1.33348729079263205789684051862, 1.43252734112867369444821905008, 1.99467673071924519083284052964, 2.13558342819319987179677717980, 2.38699024214473629990325373520, 2.53859636580750126562302320329, 2.94965216852766916943593589809, 3.15863881630859248015302078944, 3.71918597690148423338195003855, 4.00953531069221543936457938232, 4.15525070154184011536883265379, 4.39528980206370327857375512028, 4.45204434341413563628072675829, 4.81556619777009654978729339033, 5.18711442836667646978261745305, 5.40791582005776150874754034297, 5.60565149586405895933027653742, 5.94373998749367109128577814168, 6.13541030575846247905842588754, 6.16957828395956178837673688583, 6.41691801419106463507159133991, 6.67440396070481376157460128941, 6.80543419223956823452040612074